בצעירותי, כשבלעתי בשקיקה כל ספר שיכולתי למצוא על מדע וטכנולוגיה, נתקלתי לא אחת בטענה כי במתמטיקה יש יופי מופלא: אסתטיקה שאפשר להשוות אותה לזו שאנחנו יכולים למצוא בציור נהדר, במוזיקה נשגבת או אפילו במסירה גאונית בכדורגל או בכדורסל. טיעונים כמו, למשל, הציטוט הזה, של המתמטיקאי גודפרי הרדי (G. H. Hardy):
"הדפוסים של המתמטיקאי, כמו אלה של הצייר או המשורר, חייבים להיות יפים. הרעיונות [המתמטיים], כמו הצבעים או המילים, חייבים להתאים זה לזה בהרמוניה. יופי הוא המבחן הראשון [לנכונותה של טענה מתמטית]: אין מקום קבוע בעולמנו למתמטיקה מכוערת."
לרוע המזל, בכל שנותי בתיכון – ובמרבית שנותי באקדמיה – לא זכיתי לראות היופי הזה. המורים שלימדו אותי התרכזו תמיד בפרקטיקה, בפרטים הקטנים ובטכניקות, וכמעט אף אחד מהם מעולם לא טרח לעצור לרגע, לעשות 'זום-אאוט' על החומר הנלמד, ולהסביר את התמונה הגדולה. לא שאני ממעיט בחשיבותם של הפרטים הקטנים והטכניקות – ברור שהם חשובים מאוד בפני עצמם – אבל לדעתי, יצירת מוטיבציה אצל התלמידים היא אחד מעמודי היסוד של לימוד נכון. מי שלא רואה את היופי שבשירה – לא ירצה לקרוא ספרי שירה, ומי שלא מוצא יופי בציורים ובפסלים – לא ירצה לבקר במוזיאוני אומנות. באותו האופן, מי שלא ימצא יופי במתמטיקה – לא יירצה ללמוד מתמטיקה, ומי שלא רוצה ללמוד – הרבה יותר קשה ללמד אותו…
אולי גם אתם רוצים, כמוני, לגלות את היופי שבמתמטיקה? אם כן, בואו נדבר על אחד הרעיונות המתמטיים המרתקים והיפים ביותר: המספרים המרוכבים (Complex Numbers).
יקום מקביל
נאמר ואתם מכינים עוגה. מולכם ניצבת קערה, ואתם מוסיפים אליה את המרכיבים הדרושים: קמח, ביצים, מים, סוכר… אתם מערבבים את המצרכים ויוצרים את הבצק – אבל אז, קטסטרופה! גיליתם שעשיתם טעות: הכנסתם לקערה יותר מדי ביצים, והבצק שלכם לא מוצלח. מה עושים? טוב, עושה רושם שהכל אבוד. אי אפשר 'לשלוף' את הביצה העודפת מתוך הבצק המוכן: היא כבר מעורבבת עם שאר המצרכים. אין ברירה אלא לזרוק לפח את הבצק ולהתחיל מחדש…
אבל מה אם הייתי אומר לכם שיש דרך לפתור את הבעיה הזו: יש 'טריק' שמאפשר לנו להפריד את הבצק המוכן בחזרה אל המרכיבים המקוריים שלו? זה יהיה נפלא, נכון? אם נפריד את הבצק בחזרה למרכיביו, נוכל בקלות להעיף את הביצה העודפת, ולקבל בצק משובח!
ה'טריק' המדובר הוא – שימו לב – לעבור ליקום מקביל, שבו הבצק המוכן שלנו מופרד בחזרה למרכיביו. שם, ביקום המקביל, ניפטר מהביצה העודפת, ואז כשנשוב אל היקום שלנו, הבצק שלנו יהיה תקין לגמרי…
טוב, ברור שאני מדבר שטויות: אי אפשר לעבור ל"יקום מקביל", זה בלתי אפשרי. הפתרון שתיארתי הוא לא יותר מאשר פנטזיה נעימה, שלעולם לא תמומש במציאות…
האמנם?
נאמר ואתם מהנדסי חשמל, ועל השולחן מולכם מונח המעגל החשמלי הבא:
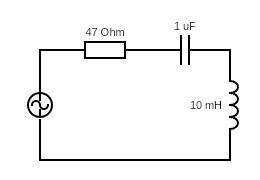
אל חשש: אני יודע שרובכם לא עוסקים בניתוח מעגלים חשמליים ושהאיור לעיל לא אומר לכם הרבה. זה בסדר – כל מה שאתם צריכים לדעת, בגדול, זה שהאיור הזה מתאר שלושה רכיבים אלקטרוניים – נגד, קבל וסליל – שמחוברים לשקע חשמל (העיגול עם סימן הגל בתוכו). לכל רכיב אלקטרוני יש ערך שנתון ביחידות מסוימות, והמתח החשמלי שמתקבל מהשקע מתנהג כמו גל סינוסי פשוט: עולה ויורד באופן מחזורי כמו גלים בבריכת גלים.
המהנדס שלנו נתבקש לחשב את הזרם הזורם במעגל החשמלי המדובר. לרוע המזל, למרות שהמעגל שמולו הוא אחד המעגלים החשמליים הפשוטים ביותר שניתן להעלות על הדעת – מדובר באתגר לא פשוט…מדוע?
ובכן, אידיאלית, המהנדס שלנו היה שמח אילו הוא היה יכול לאגד את כל שלושת הרכיבים השונים האלה, ליצור מהם רכיב אחד משותף – ואז לחשב את ההתנהגות המעגל כאילו הוא מכיל רק את הרכיב המשותף היחיד הזה, במקום שלושה רכיבים שונים. זה היה הופך את חייו של המהנדס לקלים ופשוטים.
אבל אליה וקוץ בה: הוא לא יכול לעשות זאת. מדובר בשלושה רכיבים מסוגים שונים שכל אחד מהם מגיב בצורה קצת שונה להשפעתו של מתח מחזורי – ומכיוון שהם שונים זה מזה, אי אפשר לחבר את שלושת הערכים שלהם ולהתייחס אליהם כאל 'רכיב אחד משותף', מאותה הסיבה שאני לא יכול לחבר שלושה ס"מ עם שלושה אינצ'. במילים אחרות, אני לא יכול לעשות משהו כמו:
R (resistance) = 47 + 10 + 1 = 58
ומכיוון שאי אפשר 'לאחד' את שלושת הרכיבים האלה, אז כדי לנתח את ההתנהגות שלהם תחת מתח מחזורי אנחנו נאלץ לפתור מערכת של שלושה משוואות דיפרנציאליות, אחת לכל רכיב. כל מי שלמד חשבון דיפרנציאלי ואינטגרלי (חדו"א, או 'אינפי') בתיכון או באוניברסיטה, יודע שזה ממש לא קל. המהנדס המסכן שלנו ייאלץ לבלות שעות ארוכות בחישובים מסובכים!…
המעגל החשמלי הזה הוא המקבילה האלקטרונית לבצק שהכנו בדוגמא הקודמת: יש לנו כאן מספר רכיבים אלקטרוניים שמשולבים זה בזה באותו המעגל כמו מצרכים מעורבבים בקערה, והמתמטיקה שאנחנו צריכים לעשות כדי להגיע לפתרון הרצוי מסובכת ומתישה כמו הניסיון להפריד בצק מוכן בחזרה למצרכים המקוריים.
אבל ההבדל בין שתי הדוגמאות – הבצק והמעגל האלקטרוני – הוא שבמקרה של המעגל האלקטרוני, אנחנו כן יכולים לעבור ל"יקום מקביל", יקום שבו אנחנו לא חייבים לפתור את הבעיה באמצעות משוואות דיפרנציאליות מסובכות ומתישות, אלא באמצעות פעולות פשוטות וקלות כגון חיבור, חיסור, כפל וחילוק. קסם של ממש!
סיקרנתי אתכם? בואו נכיר את היקום המקביל והמשונה הזה, שבו מתמטיקה מורכבת ומאתגרת הופכת – כבמטה קסם – למתטיקה פשוטה, כזו שגם תלמידים בבית ספר יסודי יכולים, עקרונית, להבין בקלות.
כיצד 'נולדים' המספרים המרוכבים?
נתחיל ביקום המתמטי המוכר והטוב, זה שמכיל את המספרים ה'רגילים' שכולנו לומדים מגיל אפס, פחות או יותר: 1, 2, 3… וכן הלאה – מספרים שאנחנו מכנים אותם בשם הצפוי 'המספרים הטבעיים.'
נאמר ויש לנו משוואה פשוטה:
(1) x – 5 = 0
מה הפתרון למשוואה הזו? זו שאלה קלה: x = 5. למעשה, הפתרונות לכל משוואות מהצורה הזו יהיו תמיד מספרים טבעיים ו'רגילים' שכאלה.
אבל מה לגבי המשוואה הבאה:
(2) x + 2 = 0
הממ…זה כבר קצת יותר מאתגר, כי המספר שהוא הפתרון של המשוואה הינו –
x = -2
המספר הזה לא שייך למשפחת המספרים הטבעיים. אחרי הכל, מישהו פעם החזיק ביד "מינוס שני תפוחים"? אוקי, בואו לא נהיה קטנוניים. הבה נגדיר משפחה חדשה של מספרים בשם 'משפחת המספרים השלמים', שתכיל בתוכה את המספרים הטבעיים המוכרים לנו – וגם את כל המספרים השליליים (וגם את הספרה אפס.)
אוקי, הכל בסדר: עם משפחת המספרים השלמים אנחנו יכולים לפתור את כל המשוואות שנראות כמו משוואות (1) ו- (2).
אבל אז אנחנו מקבלים משוואה חדשה:
(3) 2x – 1 = 0
שהפתרון לה הוא –
x = ½
אופס. ½ הוא לא מספר שלם, ולכן אינו שייך למשפחת המספרים השלמים!
טוב, אין ברירה, אנחנו חייבים להרחיב את המשפחה. ניצור משפחה חדשה בשם 'משפחת המספרים הרציונליים' (מהמילה Ratio, 'שבר' או 'יחס'), ונכלול בתוכה את כל המספרים הטבעיים, כל המספרים השלמים – ובנוסף, גם את כל השברים. בעזרת חברי משפחת המספרים הרציונליים אנחנו יכולים כעת לפתור את כל המשוואות בעולם שנראות כמו (1), (2) ו- (3).
אבל מסע התלאות שלנו לא נגמר. עכשיו קיבלנו משוואה מהצורה הבאה:
(4) x2 – 5 = 0
שהפתרון שלה הוא, שוב, מספר מסוג חדש לגמרי:
x = √5
המספר החדש הזה הוא בברור לא מספר טבעי, וגם לא מספר שלם – ואפילו לא מספר רציונלי, כי מסתבר שאי אפשר לכתוב אותו בצורת שבר. אני מניח שאתם מבינים לאן אני חותר…אין ברירה, נפשיל שרוולים וניצור משפחה חדשה: 'משפחת המספרים הממשיים'. למשפחה הזו, כמו בכל קודמותיה, שייכות כל משפחות המספרים הקיימות – בתוספת אותם מספרים מיוחדים שהם 'לא רציונליים' (דהיינו, אי אפשר לכתוב אותם כשבר.)
זהו? סיימנו? לא: עוד משוואה אחת אחרונה, מבטיח.
(5) x2 + 1 = 0
הפתרון למשוואה הזו יהיה, שוב פעם, מספר חדש לגמרי – כזה שלא שייך לאף משפחת מספרים קודמת:
x = √-1
אבל המספר החדש הזה, שורש של מינוס אחת, הוא מספר מאוד משונה. מדוע?
ובכן, את כל המספרים הקודמים שהכרנו – המספרים ששייכים למשפחת המספרים הממשיים – אפשר למקם על ציר המספרים. זאת אומרת, אם היה לנו סרגל באורך אינסופי, היינו יכולים לסמן את כל המספרים הממשיים על הסרגל הזה (הערה: כן, זה לא ממש נכון – אבל אני מעגל פינות לצורך ההסבר. תזרמו איתי.) אבל את המספר החדש הזה, שורש של מינוס אחת, אי אפשר לסמן על הסרגל, מכיוון שהוא פשוט לא קיים. חוקי האלגברה אומרים בפרוש שאי אפשר להוציא שורש של מספר שלילי. בניסוח אחר, אפשר לומר שהמספר 'שורש של מינוס אחת' לא קיים ביקום המתמטי שלנו.
כדי להקל עלינו את החיים, במקום לכתוב 'שורש של מינוס אחת' – שזה ארוך ומסורבל – נציין את המספר הזה באות i.
i = √-1
המספרים החדשים האלה מכונים 'מספרים מרוכבים', והסיבה שהם מכונים 'מרוכבים' היא מכיוון שהם עשויים משני חלקים שמחוברים יחד זה לזה, כמו רהיט להרכבה של איקאה. חלק אחד הוא "החלק הממשי" (דהיינו, מספר ששייך למשפחת המספרים הממשיים), והחלק השני הוא "החלק המדומה"- מספר שהוא כפולה כלשהי של i. ניתן לייצג מספר מרוכב באופן הבא:
(6) z = a + ib
אפשר לומר שמספרים מרוכבים מתקיימים ב"תפר" שבין שני היקומים: חלק אחד, החלק הממשי, שייך ליקום המתמטי הטוב והמוכר של המספרים הממשיים – וחלק שני, החלק המדומה, חי ביקום האחר, יקום שבו בצק יכול להיות מופרד בחזרה למרכיביו וחישובים מתמטיים מסובכים הופכים לפעולות פשוטות של חיבור וחיסור. המספרים המרוכבים, אם כן, עשויים לשמש כמעין גשר בין היקומים האלה.
המספרים המרוכבים בפעולה
בואו נראה את המספרים המרוכבים בפעולה. הבה נחזור למעגל החשמלי שהמהנדס ההיפוטתי צריך לחשב את הזרם הזורם בו.
ביקום שלנו, לנגדים, קבלים וסלילים יש ערכים שהם מספרים ממשיים. זאת אומרת, כשאני הולך לחנות ומבקש מהמוכר נגד, אני אומר לו משהו בסגנון 'תן לי נגד של 47 אוהם': אוהם היא יחידת ההתנגדות הסטנדרטית, ו-47 הוא מספר ממשי, כזה שאנחנו יכולים לסמן על סרגל ביקום שלנו.
אבל כדי להעביר את המעגל החשמלי שלי מהיקום שלנו אל היקום של המספרים המרוכבים, אני צריך להמיר את הערכים המוכרים לערכים שקולים להם במספרים מרוכבים: זה ה'טריק' שמעביר אותי בין שני היקומים. מכיוון שפיסת המידע הספציפית הזו רלוונטית רק למהנדסי חשמל, אז כדי לא לסבך לכם את החיים שלא לצורך אני לא אסביר במסגרת שורות אלה איך בדיוק עושים את ההמרה הזו: די אם תדעו שאפשר לעשות ההמרה הזו, ואפילו די בקלות.
קיבלנו, אם כן, את אותו המעגל המקורי – אבל עכשיו, ערכי הרכיבים השונים שלו כבר לא ניתנים כמספרים ממשיים – כי אם כמספרים מרוכבים. לשם ההסבר, הוספתי לדיאגרמה גם ערכים (סתמיים לגמרי, רק לשם הדוגמא):
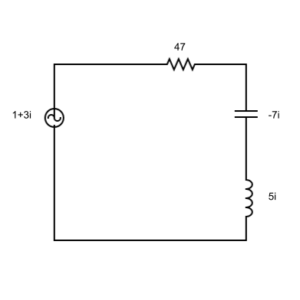
ועכשיו מגיע החלק המגניב בכל הסיפור… ביקום שלנו, היקום של המספרים הממשיים, אסור לי לחבר את שלושת הרכיבים לרכיב אחד משותף. אבל ביקום של המספרים המרוכבים, מותר לי לעשות את זה! ולא רק שמותר לי לעשות זאת, במקרה של המעגל שלנו האיחוד המדובר יהיה פעולת חיבור פשוטה וקלה:
Z = 47 – 7i + 5i = 47 -2i
או במילים אחרות, קיבלנו רכיב בודד שערכו:
Z = 47 – 2i
והוא שקול לכל שלושת הרכיבים המקוריים שלנו – דהיינו, הוא מגיב למתח מחזורי באותו האופן שבו מגיבים שלושת הרכיבים המחוברים:

כעת, המהנדס שלנו יכול לבצע את החישוב הנדרש כדי למצוא את הזרם הזורם במעגל בקלות. שוב, לא אכנס כאן להסבר לגבי האופן המדויק שבו נעשה החישוב הזה – אבל הפרט החשוב כאן הוא שהחלפנו שלושה רכיבים ברכיב וירטואלי אחד, והחלפנו חישובים מסובכים של משוואות דיפרנציאליות – בחישובי חיבור, חיסור, כפל וחילוק שכל אחד יכול לעשות בקלות.
אפילוג: מהו יופי?
בעיית פתרון המעגל החשמלי שהצגתי כאן היא רק דוגמא אחת מני רבות לאופן שבו מאפשרים לנו המספרים המרוכבים לפתור בקלות יחסית בעיות קשות ומורכבות, במגוון רחב של דיסיפלינות מדעיות והנדסיות – מהנדסת חשמל ועד פיזיקה קוונטית.
אבל מעבר לעובדה שהם שימושיים, אני גם מוצא את המספרים המרוכבים 'יפים' במובן האסתטי. מדוע? כמו תמיד, זו שאלה שקשה להשיב עליה. מה גורם לנו לומר על שיר כלשהו שהוא 'יפה', ועל שיר אחר שהוא 'פחות יפה'? מה הופך ציור לציור יפה? כל אחד רשאי לתת לשאלה הזו תשובה משלו. עבורי, מספרים מרוכבים הם יפים בגלל הניגוד המרתק שבין סדרת הצעדים הפשוטים וההגיוניים שעשינו כדי להגיע אליהם – והתוצאה המפתיעה אליה הגענו. כשדויד גילמור, הגיטריסט הגאון של פינק פלויד, מנגן בגיטרה, הוא משתמש באותם שניים עשר תווים מוזיקליים שכולנו משתמשים בהם – אבל איך שהוא, המלודיות שהוא מפיק הן נשגבות מעבר לרוב היצירות שאני מכיר. כשבוב רוס מצייר, משיכות המכחול שלו קצרות ופשוטות – אבל איפה שהוא לאורך הדרך, משיכות המכחול הקצרות האלה הופכות לפתע פתאום להר מרשים או יער קסום… באותו האופן, המסע אל המספרים המרוכבים מתחיל במספרים הטבעיים שכולנו מכירים – 1,2,3… – ומשוואות פולינומיות פשוטות, ואז לפתע אנחנו מוצאים את עצמנו במעין יקום מקביל שבו דברים שתמיד לקחנו כמובנים מאליהם לפתע פתאום מתהפכים על ראשם, והבלתי אפשרי הופך לאפשרי.
וזה יפה. מאוד, מאוד, מאוד יפה.
רן.



באמצע קריאה נהדר בינתיים, טעות סימן במשוואה 2.
תודה! אכן טעות – תוקן 🙂
התבלבל בציור הראשון כתבת H ליד הקבל וF ליד הסליל
אכן! תיקנתי. תודה, דורי 🙂
מדהים כמה פשוט לנתח את זה.
עשית לי סדר
איזה כיף! תודה, איציק 🙂
מעולה!
תודה, רונן! 🙂
שלום רב מורי ורבי, רן היקר.
אני רואטה שאתה מגיב כאן לתגובות אז זו ההזדמנות שלי להגיד לך "תודה רבה" ולספר לך כמה אתה מועיל ומוסיף לי לחיים.
אני נולדתי (ואני עדיין) חרדי, ולכן לא זכיתי לקבל חינוך אקדמאי. נמנעו ממני לימודי ליבה, ואני מנסה ומתעקש להשלים אותם.
ניסתי מכל כיוון להשלים אותם, אבל כולם כבר מתחילים מהשלב השני בעוד שלי חסר הבסיס. אתה בניגוד לכל המרצים, יודע להתחיל מא6פס בלי לפגוע במקצועיות ובנכונות של הדברים.
הפודקאסטים שלך משלימים לי הרבה מאוד ידע, בפרט הפודקאסט 'עושים היסטוריה'. אני מודה לך על העבודה שלך, וגם על המאמר הזה שהשתדלתי להבין (אם כי הפערים עדיין בעוכרי).
תודה לך.
(כולי תקווה שתראה את התגובה)
כהערה: כאמור הידיעות שלי במתמטיקה מאוד קלושות, ועדיין אני חושש שהייתי אמור להבין את המשוואה השלישית, ולא הצלחתי.
תודה, אהרן! ריגשת אותי מאוד בתגובה שלך. יש לי פינה מיוחדת בלב לנושא של קידום החברה החרדית בהקשר החינוכי, ואני מאוד מאוד שמח לשמוע שאני עוזר לך, ולו במעט 🙂 🙂
לגבי המשוואה השלישית – אני מניח שאתה מתכוון ל – 2x-1=0? אם כן, אז הנה ההסבר:
לפי כללי המתמטיקה, מותר לנו להעביר את המינוס אחת לצד השני של המשוואה, בתנאי שאנחנו הופכים את הסימן – דהיינו, את המינוס לפלוס. קיבלנו – 2x=1.
כעת נעביר את ה-2 מצד שמאל לימין. מכיוון שה-2 הוא חלק ממכפלה (2*x), כדי להעביר אותו נצטרך לחלק את שני צידי המשוואה ב-2. דהיינו: 2x/2 = 1/2.
בצד השמאלי, ה-2 במונה וה-2 במכנה מתבטלים (מכיוון ש- 2 חלקי 2 שווה אחת, ואז אנחנו מקבלים 1 כפול X, שזה שווה ל-X). קיבלנו את התוצאה הסופית: x=1/2.
מקווה שעזרתי 🙂
רן
כתבה יפה, אבל הדוגמה של היופי היא דווקא מהעולם הפרקטי.
ומה עם משוואת המהירות היחסית, כשעוברים את מהירות האור, והערך מתחת לשורש הופך לשלילי? האם אפשר לומר שאפשר לעבור את מהירות האור אם עוברים ליקום מקביל?
שאלה מרתקת! אם הבנתי את מה שרשמת, אז אתה בעצם שואל לגבי הקשר בין העולם המתמטי והעולם הפיזי: אם משהו
נכון בעולם המתמטי, האם הוא בהכרח נכון גם במציאות הגשמית?
ובכן, אני די בטוח שהיו לא מעט תגליות נעשו קודם כל במישור המתמטי – למשל, גילוי של משוואה מסוימת – ורק לאחר
מכן גילינו את התופעה הפיזיקלית המתוארת על ידי המתמטיקה. אין לי דוגמה ספציפית בראש כרגע, אבל אני חושב שאם אחפור
קצת אגלה כזו. האם זה נכון גם במקרה שתיארת? אין לי מושג, אבל תחושת הבטן שלי אומרת שכן… תורת הקוונטים
הראתה לנו שהרבה דברים שאנחנו רואים כ'לא הגיוניים' – בכל זאת קיימים. אולי זה גם ככה לגבי מהירות האור 🙂
רן