הנמלים הן אחד היצורים הכי שונים מבני האדם שאפשר לדמיין. במובנים מסוימים הן כמעט ההפך המוחלט שלנו. אז מה קורה כשאתה מנסה לקחת רעיונות ומושגים ממין אחד, שהוא כמעט חייזרי מיחס לבני האדם – ולהחיל אותם על החברה האנושית? התוצאה מפתיעה, שנויה מאד במחלוקת ואפשר גם לומר – מהפכנית.
ארדואינו: Accessory Shield – תיעוד לא רשמי
אמל"ק: מידע ותוכנות דמו עבור לוח הרחבה Accessory Shield לארדואינו, שמכיל מגוון רחב של חיישנים ואביזרים – מעולה למתחילים.

לפני מספר שבועות רכשתי לוח ארדואינו (מה זה?) ובאותה הזדמנות רכשתי גם לוח הרחבה קטן בשם Accesory Shield, ועליו מגוון רחב של חיישנים ואביזרים –
- תצוגת OLED קטנה (128×64).
- חיישן טמפרטורה
- ג'ויסטיק
- זמזם
- פוטנציומטר
- שעון Read Time
- תקשורת אלחוטית XBee.
לוח ההרחבה הזה הוא תוספת מעולה עבור מי שמתחילים את המסע שלהם עם הארדואינו: הוא מדגים את כל השימושיים הבסיסיים של הארדואינו – מתצוגה, דרך תקשורת קווית ועד שימוש בספריות.
לרוע המזל, התיעוד של הלוח הזה ודוגמאות הקוד שמלוות אותו הם די פארש – ולקח לי יותר מדי זמן להבין איך הדברים עובדים. מכיוון שכך, החלטתי לעשות סדר בבלגן וליצור תיעוד לא רשמי ודוגמאות קוד איכותיות יותר עבור לוח ההרחבה, לשימושם של מי שירכשו אותו בעתיד. את התיעוד והקוד תמצאו כאן.
בהצלחה! 🙂
רן
היופי שבמתמטיקה: מספרים מרוכבים
בצעירותי, כשבלעתי בשקיקה כל ספר שיכולתי למצוא על מדע וטכנולוגיה, נתקלתי לא אחת בטענה כי במתמטיקה יש יופי מופלא: אסתטיקה שאפשר להשוות אותה לזו שאנחנו יכולים למצוא בציור נהדר, במוזיקה נשגבת או אפילו במסירה גאונית בכדורגל או בכדורסל. טיעונים כמו, למשל, הציטוט הזה, של המתמטיקאי גודפרי הרדי (G. H. Hardy):
"הדפוסים של המתמטיקאי, כמו אלה של הצייר או המשורר, חייבים להיות יפים. הרעיונות [המתמטיים], כמו הצבעים או המילים, חייבים להתאים זה לזה בהרמוניה. יופי הוא המבחן הראשון [לנכונותה של טענה מתמטית]: אין מקום קבוע בעולמנו למתמטיקה מכוערת."
לרוע המזל, בכל שנותי בתיכון – ובמרבית שנותי באקדמיה – לא זכיתי לראות היופי הזה. המורים שלימדו אותי התרכזו תמיד בפרקטיקה, בפרטים הקטנים ובטכניקות, וכמעט אף אחד מהם מעולם לא טרח לעצור לרגע, לעשות 'זום-אאוט' על החומר הנלמד, ולהסביר את התמונה הגדולה. לא שאני ממעיט בחשיבותם של הפרטים הקטנים והטכניקות – ברור שהם חשובים מאוד בפני עצמם – אבל לדעתי, יצירת מוטיבציה אצל התלמידים היא אחד מעמודי היסוד של לימוד נכון. מי שלא רואה את היופי שבשירה – לא ירצה לקרוא ספרי שירה, ומי שלא מוצא יופי בציורים ובפסלים – לא ירצה לבקר במוזיאוני אומנות. באותו האופן, מי שלא ימצא יופי במתמטיקה – לא יירצה ללמוד מתמטיקה, ומי שלא רוצה ללמוד – הרבה יותר קשה ללמד אותו…
אולי גם אתם רוצים, כמוני, לגלות את היופי שבמתמטיקה? אם כן, בואו נדבר על אחד הרעיונות המתמטיים המרתקים והיפים ביותר: המספרים המרוכבים (Complex Numbers).
יקום מקביל
נאמר ואתם מכינים עוגה. מולכם ניצבת קערה, ואתם מוסיפים אליה את המרכיבים הדרושים: קמח, ביצים, מים, סוכר… אתם מערבבים את המצרכים ויוצרים את הבצק – אבל אז, קטסטרופה! גיליתם שעשיתם טעות: הכנסתם לקערה יותר מדי ביצים, והבצק שלכם לא מוצלח. מה עושים? טוב, עושה רושם שהכל אבוד. אי אפשר 'לשלוף' את הביצה העודפת מתוך הבצק המוכן: היא כבר מעורבבת עם שאר המצרכים. אין ברירה אלא לזרוק לפח את הבצק ולהתחיל מחדש…
אבל מה אם הייתי אומר לכם שיש דרך לפתור את הבעיה הזו: יש 'טריק' שמאפשר לנו להפריד את הבצק המוכן בחזרה אל המרכיבים המקוריים שלו? זה יהיה נפלא, נכון? אם נפריד את הבצק בחזרה למרכיביו, נוכל בקלות להעיף את הביצה העודפת, ולקבל בצק משובח!
ה'טריק' המדובר הוא – שימו לב – לעבור ליקום מקביל, שבו הבצק המוכן שלנו מופרד בחזרה למרכיביו. שם, ביקום המקביל, ניפטר מהביצה העודפת, ואז כשנשוב אל היקום שלנו, הבצק שלנו יהיה תקין לגמרי…
טוב, ברור שאני מדבר שטויות: אי אפשר לעבור ל"יקום מקביל", זה בלתי אפשרי. הפתרון שתיארתי הוא לא יותר מאשר פנטזיה נעימה, שלעולם לא תמומש במציאות…
האמנם?
נאמר ואתם מהנדסי חשמל, ועל השולחן מולכם מונח המעגל החשמלי הבא:
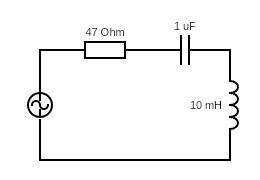
אל חשש: אני יודע שרובכם לא עוסקים בניתוח מעגלים חשמליים ושהאיור לעיל לא אומר לכם הרבה. זה בסדר – כל מה שאתם צריכים לדעת, בגדול, זה שהאיור הזה מתאר שלושה רכיבים אלקטרוניים – נגד, קבל וסליל – שמחוברים לשקע חשמל (העיגול עם סימן הגל בתוכו). לכל רכיב אלקטרוני יש ערך שנתון ביחידות מסוימות, והמתח החשמלי שמתקבל מהשקע מתנהג כמו גל סינוסי פשוט: עולה ויורד באופן מחזורי כמו גלים בבריכת גלים.
המהנדס שלנו נתבקש לחשב את הזרם הזורם במעגל החשמלי המדובר. לרוע המזל, למרות שהמעגל שמולו הוא אחד המעגלים החשמליים הפשוטים ביותר שניתן להעלות על הדעת – מדובר באתגר לא פשוט…מדוע?
ובכן, אידיאלית, המהנדס שלנו היה שמח אילו הוא היה יכול לאגד את כל שלושת הרכיבים השונים האלה, ליצור מהם רכיב אחד משותף – ואז לחשב את ההתנהגות המעגל כאילו הוא מכיל רק את הרכיב המשותף היחיד הזה, במקום שלושה רכיבים שונים. זה היה הופך את חייו של המהנדס לקלים ופשוטים.
אבל אליה וקוץ בה: הוא לא יכול לעשות זאת. מדובר בשלושה רכיבים מסוגים שונים שכל אחד מהם מגיב בצורה קצת שונה להשפעתו של מתח מחזורי – ומכיוון שהם שונים זה מזה, אי אפשר לחבר את שלושת הערכים שלהם ולהתייחס אליהם כאל 'רכיב אחד משותף', מאותה הסיבה שאני לא יכול לחבר שלושה ס"מ עם שלושה אינצ'. במילים אחרות, אני לא יכול לעשות משהו כמו:
R (resistance) = 47 + 10 + 1 = 58
ומכיוון שאי אפשר 'לאחד' את שלושת הרכיבים האלה, אז כדי לנתח את ההתנהגות שלהם תחת מתח מחזורי אנחנו נאלץ לפתור מערכת של שלושה משוואות דיפרנציאליות, אחת לכל רכיב. כל מי שלמד חשבון דיפרנציאלי ואינטגרלי (חדו"א, או 'אינפי') בתיכון או באוניברסיטה, יודע שזה ממש לא קל. המהנדס המסכן שלנו ייאלץ לבלות שעות ארוכות בחישובים מסובכים!…
המעגל החשמלי הזה הוא המקבילה האלקטרונית לבצק שהכנו בדוגמא הקודמת: יש לנו כאן מספר רכיבים אלקטרוניים שמשולבים זה בזה באותו המעגל כמו מצרכים מעורבבים בקערה, והמתמטיקה שאנחנו צריכים לעשות כדי להגיע לפתרון הרצוי מסובכת ומתישה כמו הניסיון להפריד בצק מוכן בחזרה למצרכים המקוריים.
אבל ההבדל בין שתי הדוגמאות – הבצק והמעגל האלקטרוני – הוא שבמקרה של המעגל האלקטרוני, אנחנו כן יכולים לעבור ל"יקום מקביל", יקום שבו אנחנו לא חייבים לפתור את הבעיה באמצעות משוואות דיפרנציאליות מסובכות ומתישות, אלא באמצעות פעולות פשוטות וקלות כגון חיבור, חיסור, כפל וחילוק. קסם של ממש!
סיקרנתי אתכם? בואו נכיר את היקום המקביל והמשונה הזה, שבו מתמטיקה מורכבת ומאתגרת הופכת – כבמטה קסם – למתטיקה פשוטה, כזו שגם תלמידים בבית ספר יסודי יכולים, עקרונית, להבין בקלות.
כיצד 'נולדים' המספרים המרוכבים?
נתחיל ביקום המתמטי המוכר והטוב, זה שמכיל את המספרים ה'רגילים' שכולנו לומדים מגיל אפס, פחות או יותר: 1, 2, 3… וכן הלאה – מספרים שאנחנו מכנים אותם בשם הצפוי 'המספרים הטבעיים.'
נאמר ויש לנו משוואה פשוטה:
(1) x – 5 = 0
מה הפתרון למשוואה הזו? זו שאלה קלה: x = 5. למעשה, הפתרונות לכל משוואות מהצורה הזו יהיו תמיד מספרים טבעיים ו'רגילים' שכאלה.
אבל מה לגבי המשוואה הבאה:
(2) x + 2 = 0
הממ…זה כבר קצת יותר מאתגר, כי המספר שהוא הפתרון של המשוואה הינו –
x = -2
המספר הזה לא שייך למשפחת המספרים הטבעיים. אחרי הכל, מישהו פעם החזיק ביד "מינוס שני תפוחים"? אוקי, בואו לא נהיה קטנוניים. הבה נגדיר משפחה חדשה של מספרים בשם 'משפחת המספרים השלמים', שתכיל בתוכה את המספרים הטבעיים המוכרים לנו – וגם את כל המספרים השליליים (וגם את הספרה אפס.)
אוקי, הכל בסדר: עם משפחת המספרים השלמים אנחנו יכולים לפתור את כל המשוואות שנראות כמו משוואות (1) ו- (2).
אבל אז אנחנו מקבלים משוואה חדשה:
(3) 2x – 1 = 0
שהפתרון לה הוא –
x = ½
אופס. ½ הוא לא מספר שלם, ולכן אינו שייך למשפחת המספרים השלמים!
טוב, אין ברירה, אנחנו חייבים להרחיב את המשפחה. ניצור משפחה חדשה בשם 'משפחת המספרים הרציונליים' (מהמילה Ratio, 'שבר' או 'יחס'), ונכלול בתוכה את כל המספרים הטבעיים, כל המספרים השלמים – ובנוסף, גם את כל השברים. בעזרת חברי משפחת המספרים הרציונליים אנחנו יכולים כעת לפתור את כל המשוואות בעולם שנראות כמו (1), (2) ו- (3).
אבל מסע התלאות שלנו לא נגמר. עכשיו קיבלנו משוואה מהצורה הבאה:
(4) x2 – 5 = 0
שהפתרון שלה הוא, שוב, מספר מסוג חדש לגמרי:
x = √5
המספר החדש הזה הוא בברור לא מספר טבעי, וגם לא מספר שלם – ואפילו לא מספר רציונלי, כי מסתבר שאי אפשר לכתוב אותו בצורת שבר. אני מניח שאתם מבינים לאן אני חותר…אין ברירה, נפשיל שרוולים וניצור משפחה חדשה: 'משפחת המספרים הממשיים'. למשפחה הזו, כמו בכל קודמותיה, שייכות כל משפחות המספרים הקיימות – בתוספת אותם מספרים מיוחדים שהם 'לא רציונליים' (דהיינו, אי אפשר לכתוב אותם כשבר.)
זהו? סיימנו? לא: עוד משוואה אחת אחרונה, מבטיח.
(5) x2 + 1 = 0
הפתרון למשוואה הזו יהיה, שוב פעם, מספר חדש לגמרי – כזה שלא שייך לאף משפחת מספרים קודמת:
x = √-1
אבל המספר החדש הזה, שורש של מינוס אחת, הוא מספר מאוד משונה. מדוע?
ובכן, את כל המספרים הקודמים שהכרנו – המספרים ששייכים למשפחת המספרים הממשיים – אפשר למקם על ציר המספרים. זאת אומרת, אם היה לנו סרגל באורך אינסופי, היינו יכולים לסמן את כל המספרים הממשיים על הסרגל הזה (הערה: כן, זה לא ממש נכון – אבל אני מעגל פינות לצורך ההסבר. תזרמו איתי.) אבל את המספר החדש הזה, שורש של מינוס אחת, אי אפשר לסמן על הסרגל, מכיוון שהוא פשוט לא קיים. חוקי האלגברה אומרים בפרוש שאי אפשר להוציא שורש של מספר שלילי. בניסוח אחר, אפשר לומר שהמספר 'שורש של מינוס אחת' לא קיים ביקום המתמטי שלנו.
כדי להקל עלינו את החיים, במקום לכתוב 'שורש של מינוס אחת' – שזה ארוך ומסורבל – נציין את המספר הזה באות i.
i = √-1
המספרים החדשים האלה מכונים 'מספרים מרוכבים', והסיבה שהם מכונים 'מרוכבים' היא מכיוון שהם עשויים משני חלקים שמחוברים יחד זה לזה, כמו רהיט להרכבה של איקאה. חלק אחד הוא "החלק הממשי" (דהיינו, מספר ששייך למשפחת המספרים הממשיים), והחלק השני הוא "החלק המדומה"- מספר שהוא כפולה כלשהי של i. ניתן לייצג מספר מרוכב באופן הבא:
(6) z = a + ib
אפשר לומר שמספרים מרוכבים מתקיימים ב"תפר" שבין שני היקומים: חלק אחד, החלק הממשי, שייך ליקום המתמטי הטוב והמוכר של המספרים הממשיים – וחלק שני, החלק המדומה, חי ביקום האחר, יקום שבו בצק יכול להיות מופרד בחזרה למרכיביו וחישובים מתמטיים מסובכים הופכים לפעולות פשוטות של חיבור וחיסור. המספרים המרוכבים, אם כן, עשויים לשמש כמעין גשר בין היקומים האלה.
המספרים המרוכבים בפעולה
בואו נראה את המספרים המרוכבים בפעולה. הבה נחזור למעגל החשמלי שהמהנדס ההיפוטתי צריך לחשב את הזרם הזורם בו.
ביקום שלנו, לנגדים, קבלים וסלילים יש ערכים שהם מספרים ממשיים. זאת אומרת, כשאני הולך לחנות ומבקש מהמוכר נגד, אני אומר לו משהו בסגנון 'תן לי נגד של 47 אוהם': אוהם היא יחידת ההתנגדות הסטנדרטית, ו-47 הוא מספר ממשי, כזה שאנחנו יכולים לסמן על סרגל ביקום שלנו.
אבל כדי להעביר את המעגל החשמלי שלי מהיקום שלנו אל היקום של המספרים המרוכבים, אני צריך להמיר את הערכים המוכרים לערכים שקולים להם במספרים מרוכבים: זה ה'טריק' שמעביר אותי בין שני היקומים. מכיוון שפיסת המידע הספציפית הזו רלוונטית רק למהנדסי חשמל, אז כדי לא לסבך לכם את החיים שלא לצורך אני לא אסביר במסגרת שורות אלה איך בדיוק עושים את ההמרה הזו: די אם תדעו שאפשר לעשות ההמרה הזו, ואפילו די בקלות.
קיבלנו, אם כן, את אותו המעגל המקורי – אבל עכשיו, ערכי הרכיבים השונים שלו כבר לא ניתנים כמספרים ממשיים – כי אם כמספרים מרוכבים. לשם ההסבר, הוספתי לדיאגרמה גם ערכים (סתמיים לגמרי, רק לשם הדוגמא):
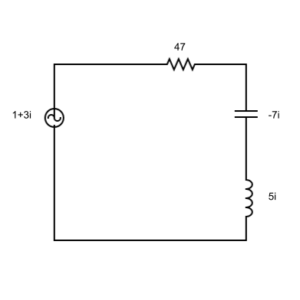
ועכשיו מגיע החלק המגניב בכל הסיפור… ביקום שלנו, היקום של המספרים הממשיים, אסור לי לחבר את שלושת הרכיבים לרכיב אחד משותף. אבל ביקום של המספרים המרוכבים, מותר לי לעשות את זה! ולא רק שמותר לי לעשות זאת, במקרה של המעגל שלנו האיחוד המדובר יהיה פעולת חיבור פשוטה וקלה:
Z = 47 – 7i + 5i = 47 -2i
או במילים אחרות, קיבלנו רכיב בודד שערכו:
Z = 47 – 2i
והוא שקול לכל שלושת הרכיבים המקוריים שלנו – דהיינו, הוא מגיב למתח מחזורי באותו האופן שבו מגיבים שלושת הרכיבים המחוברים:

כעת, המהנדס שלנו יכול לבצע את החישוב הנדרש כדי למצוא את הזרם הזורם במעגל בקלות. שוב, לא אכנס כאן להסבר לגבי האופן המדויק שבו נעשה החישוב הזה – אבל הפרט החשוב כאן הוא שהחלפנו שלושה רכיבים ברכיב וירטואלי אחד, והחלפנו חישובים מסובכים של משוואות דיפרנציאליות – בחישובי חיבור, חיסור, כפל וחילוק שכל אחד יכול לעשות בקלות.
אפילוג: מהו יופי?
בעיית פתרון המעגל החשמלי שהצגתי כאן היא רק דוגמא אחת מני רבות לאופן שבו מאפשרים לנו המספרים המרוכבים לפתור בקלות יחסית בעיות קשות ומורכבות, במגוון רחב של דיסיפלינות מדעיות והנדסיות – מהנדסת חשמל ועד פיזיקה קוונטית.
אבל מעבר לעובדה שהם שימושיים, אני גם מוצא את המספרים המרוכבים 'יפים' במובן האסתטי. מדוע? כמו תמיד, זו שאלה שקשה להשיב עליה. מה גורם לנו לומר על שיר כלשהו שהוא 'יפה', ועל שיר אחר שהוא 'פחות יפה'? מה הופך ציור לציור יפה? כל אחד רשאי לתת לשאלה הזו תשובה משלו. עבורי, מספרים מרוכבים הם יפים בגלל הניגוד המרתק שבין סדרת הצעדים הפשוטים וההגיוניים שעשינו כדי להגיע אליהם – והתוצאה המפתיעה אליה הגענו. כשדויד גילמור, הגיטריסט הגאון של פינק פלויד, מנגן בגיטרה, הוא משתמש באותם שניים עשר תווים מוזיקליים שכולנו משתמשים בהם – אבל איך שהוא, המלודיות שהוא מפיק הן נשגבות מעבר לרוב היצירות שאני מכיר. כשבוב רוס מצייר, משיכות המכחול שלו קצרות ופשוטות – אבל איפה שהוא לאורך הדרך, משיכות המכחול הקצרות האלה הופכות לפתע פתאום להר מרשים או יער קסום… באותו האופן, המסע אל המספרים המרוכבים מתחיל במספרים הטבעיים שכולנו מכירים – 1,2,3… – ומשוואות פולינומיות פשוטות, ואז לפתע אנחנו מוצאים את עצמנו במעין יקום מקביל שבו דברים שתמיד לקחנו כמובנים מאליהם לפתע פתאום מתהפכים על ראשם, והבלתי אפשרי הופך לאפשרי.
וזה יפה. מאוד, מאוד, מאוד יפה.
רן.
בית הספר של העתיד
אמל"ק: מערכת החינוך הנוכחית אינה יעילה דייה ואינה מספקת רמה חינוכית גבוהה לכלל התלמידים במידה שווה. ניתן להעזר ביו-טיוב ומערכות דומות כדי לשפר אותה במידה משמעותית, תוך ניצול מיטבי של זמנם וכישוריהם של המורים.
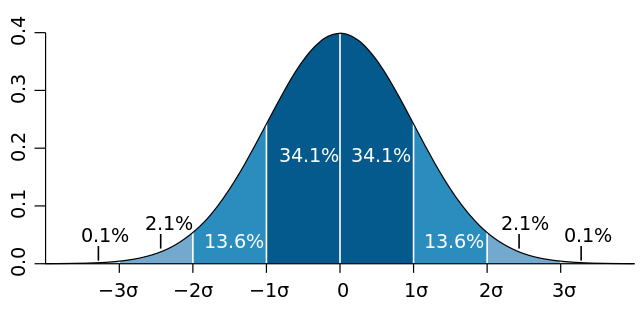
בכל מוסד חינוכי – בין אם בית ספר יסודי, חטיבת ביניים, תיכון או אפילו אוניברסיטה – יש מורים טובים יותר, ומורים טובים פחות. אין כאן ניסיון לפגוע או להעליב את המורים, חס וחלילה, או להציע על כשל כלשהו במערכת סינון המועדים למקצוע ההוראה: זו עובדה אובייקטיבית – או במילים אחרות, ככה העולם עובד. קחו אלף כדורגלנים: ברור שחלק מהם יהיו מעולים וחלק פחות. קחו אלף מדענים: חלק יהיו טובים, חלק פחות. אלף ציירים? אלף שפים? אותו הדבר. לתופעה הזו יש אפילו שם – 'התפלגות נורמלית' – והיא מיוצגת לרוב באמצעות גרף שמזכיר בצורתו פעמון. המורים המעולים, המצויינים, אלה שכל התלמידים היו בוחרים בהם לו הייתה ניתנת בידם האפשרות, נמצאים בשולי הפעמון – ומכאן שהם מהווים רק מיעוט מקרב כלל המורים. שוב, אין כאן כשל: זו ההתפלגות ה'נורמלית', במובן של – זו דרכו של עולם. חלק מהמורים יהיו ממש גרועים (אלו השוליים השמאליים של הגרף), רובם יהיו בינוניים – ומיעוטם מוצלחים.
אם אתם מחפשים עדות מוחשית לתופעה הזו, אני מציע סיור קצר בין כיתות הלימוד בטכניון. בבתי הספר, לתלמידים אין אפשרות לבחור את המורים שילמדו אותם – המורה שקיבלת הוא המורה שילמד אותך, וזהו – אבל בטכניון (ואולי גם בשאר מוסדות ההשכלה הגבוהה) יש לסטודנטים זכות בחירה שכזו. והתוצאה? כמעט בכל תחום יש מרצה אחד או שניים שהכיתה או האולם שלהם מפוצצים בסטודנטים – ושאר המרצים מלמדים מול כיתות חצי-ריקות. מדוע? מכיוון שכולם רוצים ללמוד אצל המורה הטוב, כמובן. אני די בטוח שאם היינו מאפשרים גם לתלמידי בית הספר לבחור את המורים שלהם, התוצאה הייתה דומה למדי.
אני בטוח שכולנו, הורים ומורים כאחד, היינו שמחים לו היינו יכולים לגרום לכך שכל (או לפחות רוב) המורים במערכת יהיו מוצלחים ונהדרים. איך אפשר לעשות זאת?
אפשרות אחת היא לשפר את מערכת הסינון וההכשרה של המורים, כדי שתפיק מורים טובים יותר. אבל איך עושים את זה? האם יש מישהו שיודע בוודאות איך לקחת אדם אקראי ולהפוך אותו למצוין? אני לא מדבר כאן רק על הוראה – אלא על כל תחום שנבחר. האם יש בית ספר לכדורגל שכל בוגריו טובים כמו מסי ורונאלדו? האם יש בית ספר למוזיקה שכל הנגנים שיוצאים ממנו הם וירטואוזים? התשובה היא לא. אין כזה – לא בכדורגל, לא במוזיקה וגם לא בהוראה. כמובן שבית ספר טוב יוציא מקרבו בוגרים טובים יותר בממוצע, אבל לא כולם יהיו מעולים.
רעיון נוסף שעולה בדיונים אודות שיפור רמת ההוראה בישראל הוא להעלות את שכרם של המורים כדי למשוך אנשים מצויינים למערכת החינוך. אני חושב שזה רעיון נהדר: מערכת החינוך היא חיונית לעתיד המדינה, וחשוב מאוד להביא אליה את האנשים הטובים ביותר שאנחנו יכולים למצוא. אבל האם העלאת שכרם של המורים תביא לכך שכל (או לפחות רוב) התלמידים בישראל יזכו ללמוד תחת מורים מעולים? לא. הסיבה לכך היא פשוטה ומעשית: יש למעלה מחמשת אלפים בתי ספר בישראל, שבכל אחד מהם מאות או אלפי תלמידים, שכל אחד מהם לומד כמה וכמה מקצועות. אין שום תרחיש מעשי שבו המדינה תוכל להרשות לעצמה להביא לכל אחד מבתי הספר האלה, בכל אחד מהמקצועות השונים, את המורים המעולים האלה. לא רק שאין למדינה מספיק כסף להרשות את זה לעצמה, גם סביר להניח שאין מספיק מורים מעולים שכאלה בישראל כולה! שוב, אין כאן כשל ואין כאן תקלה: זו דרכו של עולם.
אם זה המצב, ומערכת החינוך שלנו מאוכלסת ברובה על ידי מורים בינוניים – מדוע אנחנו מוכנים לקבל את המצב הזה? התשובה היא שעד לא מכבר, זו הייתה האפשרות הטובה והיעילה ביותר לחנך כמויות גדולות של ילדים ולהעניק להם השכלה בסיסית. בעידן שלפני המהפכה התעשייתית, רק משפחות אמידות מאוד יכלו להרשות לעצמן לשכור מורה פרטי שיעניק חינוך טוב לילדיהם. מערכת החינוך המודרנית אמנם מתפשרת על איכות ההוראה, אבל בתמורה מאפשרת לנו להעניק השכלה סבירה לכל הילדים, עניים ועשירים כאחד.
סינון באמצעות ההמון
אבל כיום יש לנו אפשרות טובה ויעילה עוד יותר. נקרא לאפשרות הזו "יוטיוב" – אבל אני לא מתכוון לאתר הספציפי, זה שבבעלותה של גוגל, אלא לרעיון העקרוני שמאחוריו. מיד תבינו.
ישנם מיליארדי סרטונים ביוטיוב (300 שעות של סרטונים חדשים מועלים לאתר בכל דקה!). על כל נושא שנבחר – מאלגברה ליניארית ועד שיפוץ של מכוניות עתיקות – אפשר למצוא אלפי ועשרות אלפי סרטונים. גם כאן, עקומת הפעמון עושה את עבודתה: חלק מהסרטונים האלה יהיו באיכות נמוכה, רובם יהיו בינוניים ורק מיעוטם יהיו מוצלחים ממש. אם לא הייתה למשתמשים שום דרך לברור את הסרטונים הגרועים מהטובים, סביר להניח שחוויית השימוש שלהם באתר הייתה הרבה יותר גרועה ויוטיוב לא הייתה זוכה לפופלריות הנוכחית שלה.
למזלנו, מהנדסיה של יוטיוב פיתחו מגוון דרכים ושיטות כדי לברור את הסרטונים המוצלחים מבין כלל הסרטונים. למשל, הצופים יכולים 'לאהוב' (Like) או 'לא לאהוב' (Dislike) סרטון, לשתף עם חבריהם סרטון שאהבו, להגיב על הסרטונים ולאגד אותם ברשימות צפייה (Play lists) של סרטונים מומלצים – והמערכות האוטומטיות של יוטיוב יודעות לשקלל את כל האיתותים האלה, ו'להציף' כלפי מעלה את הסרטונים הטובים יותר, אלה ששווה לנו להקדיש להם תשומת לב.
התוצאה, בשורה התחתונה, היא שאם נחפש ביוטיוב 'איך פותרים משוואה ריבועית' – נקבל סרטון שמסביר בצורה מוצלחת במיוחד איך פותרים משוואה ריבועית, ואם נחפש 'המרד הערבי הגדול' – נמצא את הסרטון שמספר על ההיסטוריה הזו בצורה המוצלחת ביותר. במילים אחרות, מצאנו את הקצה הימני של עקומת הפעמון – את המורים הטובים ביותר לאותם תחומים ונושאי לימוד שחיפשנו. כמובן שאלו אינם 'מורים' במובן המקובל של המילה, אבל אלו בכל זאת מורים לכל דבר ועניין: יוצרים שהשקיעו שעות רבות ביצירת מערך שיעור סביב נושא מסוים, והם כל כך מוכשרים עד שמבין כל אלפי הסרטונים שעוסקים באותו הנושא – הסרטון שלהם זכה להכי הרבה המלצות ושיתופים. אפשר לומר שהסרטונים המוצלחים האלה הם המקבילה האינטרנטית למרצה בשר ודם שאולם ההרצאות שלו מלא עד אפס מקום.
לסרטונים המקוונים יש תכונה חשובה נוספת: הם זמינים לכולם. בכל מקום, ובכל זמן. לא משנה אם אתה תלמיד בפריפריה או בתיכון תל-אביבי, ולא משנה אם הסרטון המדובר צולם שלשום או לפני עשרים שנה – כולם יכולים להנות מחומרי הלימוד האיכותיים האלה, בעלות אפסית: התלמידים יכולים לצפות יחד בסרטון באמצעות מקרן, או ישירות מהטלפונים החכמים שלהם.
וזה לא הכל. אמרתי מקודם שאני משתמש במילה 'יוטיוב' במובן כללי ועקרוני יותר – והמובן הזה מתייחס לשתי התכונות שציינתי: תוכן שעובר דירוג על ידי המוני משתמשים, והוא גם זמין לכל אחד ובכל זמן. ואכן, מערכות דירוג תכנים נפוצות מאוד ברחבי הרשת, יוטיוב היא לא היחידה, כמובן: מערכות דירוג שכאלה נפוצות מאוד באינטרנט, ורלוונטיות למגוון סוגי תכנים – מפודקאסטים ועד לפוסטים בבלוגים.
עובדה זו נותנת בידינו עוד תכונה חשובה של בית הספר של העתיד: לימוד פרסונלי. אין חובה שהתלמיד ילמד על המרד הערבי הגדול רק מתוך סרטון יוטיוב, אם אופן הלימוד הזה אינו מתאים לו או לה: סביר מאוד להניח שנמצא את אותם התכנים גם במדיות אחרות – בין אם קוליות, טקסטואליות או בכל דרך אחרת. עבור כל מדיה אחרת שנבחר, העקרון המנחה חייב להיות זהה –
- תוכן שעבר סינון על ידי ההמון, וגם
- תוכן שזמין לכל אחד ובכל זמן.
איך זה עובד?
מה כל זה אומר? זה אומר שאם נעבור משיטת הלימוד הנוכחית, שבה מורה עומד מול כיתה של שלושים תלמידים ומלמד אותם נושא מסוים, ללימוד באמצעות תכנים מבוססי-אינטרנט – נוכל להנות מכל העולמות:
- כל תלמיד יהנה מהמורה הכי טוב בעולם (או משהו מאוד קרוב לזה) בנושא הספציפי שאותו הוא לומד.
- כל התלמידים במדינה, ללא הבדל דת, גזע, מין ומצב כלכלי, יוכלו להנות מרמת לימודים זהה.
- זהו פתרון יעיל וזול, שעלותו תהיה שברירי אחוז מעלותה של מערכת החינוך הנוכחית.
הבה נקשור את כל הקצוות הללו, ונשרטט בדמיוננו שיעור טיפוסי בבית הספר של העתיד:
המחנכת נכנסת לכיתה. "שלום, כיתה ז' 4." היא אומרת לתלמידים שיושבים מולה, ולתלמידים שנמצאים בבית ופניהם מוקרנות על הקיר: בבית הספר של העתיד, ההבדלים בין למידה בכיתה ולמידה מרחוק מצטמצמים מאוד – שכן כולם מקבלים גישה זהה לחומרי הלימוד.
"היום נלמד על גילוי אמריקה. שלחתי לכם למייל את הקישורים לשיעור של היום." היא אומרת לתלמידים. התלמידים שולפים את הטלפונים החכמים שלהם, ובתיבת הדואר האלקטרוני ממתינים להם רשימת קישורים. קישור אחד מפנה סרטון של יוטיובר שזכה לעשרה מיליון צפיות, בעיקר בזכות האנימציות המושקעות שיצר: הסרטון זכה לתרגום רשמי שהפיק משרד החינוך, ואפילו גרסה מדובבת לעברית למי שמתקשים לעקוב אחר הכתוביות. הקישור השני הוא לפרק של הפודקאסט 'תגליות גדולות' – אחד הפודקאסטים המושקעים והאיכותיים בשפה העברית – שמספר את סיפורו של קולומבוס כדרמה חובקת עולם, והקישור השלישי הוא לסדרת פוסטים מתורגמים מהבלוג "היסטוריה מדליקה", שלאחרונה זכה בפרס מיוחד מטעם האו"ם על מצויינות בחינוך.
כל אחד מהתלמידים בוחר את המדיה המועדפת עליו, ובמשך עשרים הדקות הבאות התלמידים צופים, מאזינים וקוראים את החומר. בזמן זה, המחנכת עוברת בין הילדים, משוחחת עימם ושואלת לשלומם. אחד הבנים, היא רואה, נראה עצוב ולא מרוכז. היא מתיישבת לצידו ושואלת לשלומו: התלמיד יוכל להשלים את חומר הלימוד מאוחר יותר, בכל זמן שירצה. מסתבר שארצ'י, כלבו האהוב, הלך לאיבוד. המורה מעודדת את התלמיד, והם אפילו מנסחים יחד מודעה שהתלמיד יתלה על לוחות המודעות אחר הצהריים. כשהיא חוזרת לעמוד על רגליה, המורה מרגישה סיפוק גדול, מצב רוחו של התלמיד כבר מעודד יותר והוא מסוגל להתרכז בחומר הלימוד – ובין השניים נוצר קשר אנושי חם ועמוק יותר, שוודאי יסייע לשניהם בהמשך השנה.
"אוקי, להניח את הטלפונים בצד." מכריזה המורה, "בואו נעבור על החומר. מי יודע לומר לי באיזו שנה יצא קולומבוס למסעו?…" התלמידים והמורה משוחחים על החומר שלמדו זה עתה, פותרים שאלות וכדומה.
שאלות ותשובות
שאלה: מה נעשה עם המורים הקיימים? האם הם מיותרים?
תשובה: לא, הם אינם מיותרים. ההפך הוא הנכון: יש להם תפקיד חשוב מאוד בבית הספר של העתיד. ראשית, נזכור שהסרטונים, הפודקאסטים והבלוגים אינם אינטראקטיבים. אם לתלמיד יש שאלה – מישהו צריך להיות שם כדי לענות לו עליה. בנוסף, לימוד פאסיבי אינו מספיק: צריך גם לתרגל את החומר – לפתור תרגילים ולענות על שאלות. המורה האנושי צריך להיות זה שנותן לתלמידים את התרגילים האלה ופותר אותם יחד עימם. ולבסוף, מורה טוב הוא יותר ממורה – הוא גם מחנך, במובן העמוק של המילה. המורים בבית הספר יוכלו להקדיש את זמנם ותשומת ליבם לתלמידים עצמם, לסייע להם במצבי משבר ולהוות עבורם השראה. במילים אחרות – המורים יישארו, אבל תפקידם במערכת החינוך ישתנה.
שאלה: ומה לגבי מקצועות ונושאים שייחודיים לישראל, ואינם נפוצים באינטרנט?
תשובה: מן הסתם יהיו תחומים שעבורם יהיה קשה למצוא מגוון רחב של חומרי לימוד איכותיים באינטרנט. כמה תחומים כאלה? קשה לדעת, אבל אני מניח שלא הרבה: מרבית תחומי הלימוד בבית הספר – שפות, היסטוריה, גיאוגרפיה, מתמטיקה, פיזיקה, ביולוגיה וכו' וכו' – הם אוניברסליים, וחומר הלימוד בישראל לא צריך להיות שונה מהותית מזה שמקובל באירופה או בארצות הברית, לצורך העניין. אבל במקרים הנדירים שבהם אין מספיק חומר זמין באינטרנט, תמיד ניתן לחזור לשיטת הלימוד הפרונטלית הקלאסית. העלות הכוללת עדיין תהיה זניחה ביחס למצב הנוכחי.
שאלה: האם יוצרי התכנים לא ירצו תשלום תמורת השימוש בתכנים שלהם?
תשובה: סביר להניח שכן, ומגיע להם שישלמו להם. זה עדיין ייצא הרבה (הרבה) יותר זול מלשלם משכורות להמון מורים.
סיכום
לסיכום, החלפת מודל הלימוד הנוכחי והמיושן במודל חדש, שבו עיקר הלימוד נעשה מתוך חומרי לימוד מקוונים שעברו סינון מוקדם על ידי קהל רב ככל האפשר, נרוויח את היתרונות הבאים:
- כל התלמידים, בכל הארץ, יזכו למורים הטובים ביותר בכל המקצועות.
- המורים הקיימים ישובצו בתפקידים חדשים, בהן יוכלו להביא לידי ביטוי טוב את הצדדים 'הרכים' של המקצוע.
- המורים יהיו פנויים וזמינים יותר לסייע לתלמידים לכל צורך.
מה דעתכם? אשמח למשוב והערות בתגובות.
רן
ממה עשויים אקורדים?
הקדמה
כשהייתי נער מתבגר, למדתי לנגן על גיטרה קלאסית. כמו צעירים רבים, התחלתי לבד: מצאתי ספר ללימוד גיטרה, והתאמנתי על השירים הפשוטים-יחסית שהופיעו בו. אבל אחרי כמעט שנה של לימוד עצמי, הבנתי שאני מבזבז את הזמן: למרות מאות שעות אימון הייתי 'תקוע' על שירים פשוטים, ולא הצלחתי לנגן שום דבר באמת מעניין או מורכב.
על כן, החלטתי ללמוד בקונסרבטוריון – שם לומדים מוזיקה בצורה רצינית ומעמיקה יותר. נרשמתי לשיעור פרטי אצל אחד המורים, ואכן – כבר אחרי מספר חודשים ספורים, השיפור ביכולת הנגינה שלי היה עצום! הצלחתי לנגן יצירות קלאסיות מורכבות, שלעולם לא הייתי מצליח לנגן לו המשכתי ללמוד בגפי.
…ובכל זאת, עדיין הייתי מתוסכל. מתוסכל מכיוון שלא הבנתי מה אני מנגן. התווים על הדף היו לא יותר מאשר 'כתמים' שחורים שסימנו לי איפה לשים את האצבע על צוואר הגיטרה. ניגנתי כמו תוכי שחוזר אחרי קולות שהוא שומע מבלי להבין באמת מה הוא אומר. הרגשתי שאני כמו פטיפון, שמנגן צלילים לפי גובה החריצים בתקליט – אבל לא באמת 'עושה מוזיקה'.
כעבור שנתיים, שוב חשתי שאני "תקוע": הפעם, זה היה בכל מה שקשור לנגינה עם מוזיקאים אחרים. היום, ממרחק של שלושים שנה, אני מבין שהמורה שלמדתי אצלו לא היה מורה טוב. הוא לימד אותי טכניקה בלבד, אבל לא לימד אותי מוזיקה. מכיוון שלא הבנתי מה אני מנגן – במילים אחרות, לא דיברתי את השפה המוזיקלית אלא רק חזרתי על צלילים כמו תוכי – לא הצלחתי ליצור שיתוף פעולה מוזיקלי אמיתי עם אף אחד אחר. הסקתי שמכיוון שאפילו מורה מקצועי לא הצליח לעזור לי להפוך למוזיקאי, כנראה שהבעיה נמצאת אצלי – ופרשתי סופית.
במשך שלושים שנה לא הרמתי את הגיטרה, עד שלפני כשלוש שנים – פחות או יותר בגחמה של רגע – חזרתי לנגן בגיטרה בס. הפעם, מצויד בניסיון חיים עשיר יותר והבנה עמוקה יותר של האופן שבו המוח שלי לומד דברים חדשים, החלטתי לחזור אל חידת המוזיקה – ולפצח אותה. וכצעד ראשון, החלטתי לנסות ולענות לעצמי על שאלה בסיסית אחת: ממה עשויים אקורדים?
כל גיטריסט או פסנתרן מתחיל מכיר אקורדים – או ליתר דיוק, את הצורה שלהם. כשכתוב לי על הדף C – אני יודע איפה לשים את האצבעות על צוואר הגיטרה כדי לנגן את האקורד C. אבל השאלה שאני רוצה לענות עליה היא – מדוע זו הצורה הספציפית של אקורד C? מדוע נבחרו דווקא הצלילים הספציפיים האלה כדי להרכיב מהם את האקורד C?
השאלה הזו אינה מובנת מאליה. יבוא גיטריסט מתחיל וישאל – בצדק – למה זה בכלל מעניין אותי? למה לטרוח להבין מהם הצלילים המרכיבים את האקורד, אם אפשר פשוט ללמוד בעל פה את הצורה שלהם על צוואר הגיטרה. הרי בשורה התחתונה, הצלילים שתפיק הגיטרה יהיו אותם צלילים בין אם אבין את המשמעות שלהם ובין אם לאו. אז למה לטרוח?…
יש מספר סיבות טובות לכך, אבל אולי הפשוטה בהן היא העובדה שאנחנו לא מכונות. אני יכול ללמוד עשרה אקורדים בעל פה. עשרים. מאה… אבל בסופו של דבר, יש ה-מ-ו-ן אקורדים שאפשר לנגן, וקשה מאוד (ואולי בלתי אפשרי?) לשנן את כולם. יש כמה אקורדים נפוצים מאוד שמופיעים בכמעט כל שיר – C, Am, G… – אבל יש המון אקורדים נדירים יותר, שלא נתקלים בהם בתדירות גבוהה. אחת לכמה זמן יופיע לנו בשיר כלשהו אקורד "נדיר" שכזה, כמו G#maj7 למשל – ולא נדע איך לנגן אותו בלי לחפש את הדיאגרמה שלו בגוגל. לא טוב. אם נבין ממה עשויים אקורדים – מהם הצלילים שמרכיבים כל אקורד – לעולם לא נתפס עם המכנסיים למטה, ותמיד נוכל למצוא את הצלילים האלה בזמן אמת.
ממה עשויים אקורדים?
הבה נתחיל מעובדה יסודית פשוטה: באקורד בסיסי ישנם שלושה צלילים (או שלושה תווים). זו הסיבה לשמו הרשמי של אקורד בסיסי שכזה: טריאדה (Triad), מלשון Tri-, "שלשה." למשל, האקורד C עשוי מהתווים C, E ו-G, בעוד שהאקורד G עשוי מהתווים G, B ו-D.
מטרתנו, נזכיר, היא לגלות מהם התווים של כל אקורד. מכיוון שכאמור ישנם המון אקורדים, אנחנו צריכים למצוא "דרך קיצור": חוקיות כלשהי שתאפשר לנו לנחש את שלושת התווים של אקורד מסוים, רק מתוך השם שלו – מבלי שנאלץ לזכור את התווים האלה בעל פה.
למה הכוונה? ובכן, כשהייתי קטן, אמא שלי הייתה נותנת לי לעזור לה לאפות עוגיות. היא הייתה מרדדת את הבצק עם מערוך, ואני הייתי חותך החוצה את העוגיות באמצעות תבניות קטנות: תבנית בצורת כוכב, תבנית בצורת משולש וכדומה. יכולתי, עקרונית, לחתוך החוצה את העוגיות גם ללא תבניות: לשרטט כוכב או משולש באמצעות סכין – אבל ברור שהתבניות עשו לי את החיים קלים יותר: לא הייתי צריך לדעת איך בדיוק לחתוך כל צורה, אלא רק ללחוץ את התבנית הרצויה אל הבצק – והופ, קיבלתי עוגיה בצורה הרצויה. באותו האופן, גם אנחנו נחפש תבניות שיעזרו לנו לגלות את הצלילים של כל אקורד ללא הרבה מאמץ.
אם נבחן את כל האקורדים הקיימים, נגלה שאפשר לחלק אותם לארבעה סוגים עקרוניים, או "תבניות" באנלוגיה שלנו: אקורדים מז'וריים (Major), מינוריים (Minor), מוקטנים (Diminished) ומוגדלים (Augmented). ליתר דיוק – יש עוד כמה וכמה סוגי אקורדים, אבל ארבעת הסוגים האלה הם הנפוצים והשימושיים ביותר במוזיקה המערבית ולכן נתמקד בהם.
מרחקים בין צלילים
ארבעת סוגי האקורדים נבדלים ביניהם במרחקים שבין שלושת הצלילים השונים.
זה משפט קצת משונה, למי ששומע אותו בפעם הראשונה. אנחנו רגילים לחשוב על מרחקים בהקשר של עצמים בעולם האמיתי – "הכסא נמצא במרחק של מטר אחד מהשולחן" – אבל לא קל לתפוס את הרעיון של "מרחק" בהקשר של צלילים. למזלנו, כלי הנגינה שלנו יכולים לעזור לנו לתרגם את הרעיון של "מרחק בין צלילים" ל-"מרחק בין עצמים."
נתחיל בשאלה בסיסית: מהן היחידות שעמן מודדים מרחק בין צלילים? בעולם הפיזי, אנחנו מודדים מרחקים בס"מ או מ"מ – מהי יחידת המרחק המקבילה בעולם המוזיקה?
התשובה היא: חצאי-טונים (Semitone). ניקח, למשל, את הפסנתר: בין כל שני קלידים צמודים בפסנתר, המרחק המוזיקלי הוא חצי טון אחד. לצורך הדוגמא, ניקח את התו C. התו הצמוד אליו הוא C#, שהוא הקליד השחור הצמוד אליו מצד ימין – והמרחק המוזיקלי בין C ו- C# הוא חצי טון. אותו הרעיון קיים גם בגיטרה: המרחק בין שריג לשריג על צוואר הגיטרה הוא חצי טון. למשל, התו C נמצא במיתר החמישי שריג 3, והתו C# נמצא על אותו מיתר בשריג הרביעי, משמע שריג אחד קדימה, לכיוון בסיס הצוואר.
מצויידים בידע הזה, אנחנו מסוגלים כעת למדוד מרחקים בין צלילים שונים. למשל, מהו המרחק בין התווים C ו- E? אם תספרו את השריגים (או הקלידים) בין שתי התווים, תגלו בזריזות שהמרחק ביניהם הוא ארבעה חצאי-טונים. ומה המרחק בין C ו-G? שבעה חצאי-טונים.
המוזיקאים נתנו למרווחים מסוימים שמות:
- מרווח של שלושה חצאי טונים מכונה 'טרצה קטנה' (Minor 3rd).
- מרווח של ארבעה חצאי-טונים מכונה 'טרצה גדולה' (Major 3rd).
- מרווח של שבעה חצאי-טונים מכונה 'קווינטה זכה' (Perfect 5th).
- מרווח של שישה חצאי-טונים מכונה 'קווינטה מוקטנת' (Diminished 5th), או 'טריטון'.
- מרווח של שמונה חצאי-טונים מכונה 'קווינטה מוגדלת' (Augmented 5th).
ישנם מרווחים נוספים, כמובן – אך לא נרחיב עליהם כרגע, וגם לא אבאר את פשר השמות האלה. יש להם חשיבות – אבל לא חיונית לענייננו כרגע.
וכעת נחזור למשפט המשונה: "ארבעת סוגי האקורדים נבדלים ביניהם במרחקים שבין שלושת הצלילים השונים."
אולי עכשיו נצליח להבין את פשרו. אם יש לנו שלושה צלילים, אנחנו יכולים להציב אותם במרחקים שונים זה מזה – והמרחקים שנבחר יגדירו לנו באיזה סוג של אקורד מדובר: מז'ורי, מינורי, מוקטן או מוגדל.
הנה עוד אנלוגיה שאולי תסייע לנו להבין את העניין. דמיינו עוגה בעלת שתי שכבות: שכבת שוקולד, ומעליה שכבת קצפת. אני יכול לאפות עוגה שבה שכבת השוקולד עבה מאוד, ושכבת הקצפת דקיקה – או שאני יכול לאפות את אותה העוגה, אבל הפעם עם שכבת שוקולד דקה ושכבת קצפת עבה ונדיבה. בשני המקרים מדובר באותה עוגת שכבות בסיסית – אבל ברור שהטעם שלהן יהיה שונה: העוגה עם שכבת השוקולד העבה תהיה שונה בטעמה מהעוגה עם שכבת הקצפת העבה.
עובי השכבות, באנלוגיה שלנו, הוא המרחק בין שלושת התווים בתוך האקורד. אם אני מחליט שהמרחק בין התווים הראשון והשני באקורד יהיה מרחק גדול ( = שכבת שוקולד עבה) והמרחק בין התווים השני והשלישי יהיה קצר ( = שכבת קצפת דקה), אקבל אקורד מסוג מסוים. אבל אם אבחר במרחק קצר בין התווים הראשון והשני ( = שכבת שוקולד דקה) ומרחק גדול בין השני והשלישי ( = שכבת קצפת עבה) – אקבל אקורד מסוג שונה לגמרי, שגם יישמע אחרת. למשל, אקורדים מז'וריים נשמעים "שמחים", בעוד שאקורדים מינוריים נשמעים "עצובים". הסיבה לאופי השונה היא שהמרווחים בין הצלילים ("עובי השכבות" באנלוגיה שלנו) שונים בין שני סוגי האקורדים.
האקורד המז'ורי
נתחיל עם אקורדים מז'וריים, שכתובים לרוב כאות בודדת (לדוגמה, C או D) או לעיתים כ Cmaj ו Dmaj. מהם התווים מהם עשויים האקורדים המז'וריים?
התו הראשון יהיה, תמיד, התו שלקוח משם האקורד, והוא ייקרא 'השורש'. למשל, באקורד C, תו השורש יהיה התו C.
התו השני יהיה התו במרחק של טרצה גדולה (Major 3d) מתו השורש. בכלי הנגינה שלנו, נספור ארבעה חצאי-טונים מעל התו C, ונקבל את התו E.
התו השלישי יהיה התו במרחק של קווינטה זכה (Perfect 5th) מתו השורש. בכלי הנגינה שלנו, נספור שבעה חצאי טונים מעל התו C, ונקבל את התו G.
וזה הכל: מצאנו את כל שלושת התווים מהם עשוי האקורד C! אותה תבנית – שורש, טרצה גדולה, קווינטה זכה – מאפיינת את כל האקורדים המז'וריים באשר הם. למשל, מהם הצלילים מהם עשוי האקורד המז'ורי F? שורש – F. טרצה גדולה מעל השורש (ארבעה חצאי טונים) – A#. קווינטה זכה מעל השורש (שבעה חצאי טונים) – C. שלושה צלילים באקורד הבסיסי, וזה הכל.
ייתכן ואתם שואלים את עצמכם כעת – מה הקטע של ספירת חצאי הטונים? האם בכל פעם שאתיישב מול הפסנתר או אחזיק את הגיטרה, עלי להתחיל לספור חצאי טונים כדי לגלות את התווים שעלי לנגן באקורד?
למזלנו, התשובה היא לא: יש דרך קיצור. למשל: בגיטרה, הטרצה הגדולה נמצאת תמיד מיתר אחד למטה ושריג אחד אחורה מתו השורש. הקווינטה הזכה נמצאת תמיד מיתר אחד למטה ושני שריגים קדימה מתו השורש. במילים אחרות – אם זוכרים את התבנית הקבועה ("מיתר אחד למטה, שריג אחד אחורה"), אפשר למצוא את התו המבוקש גם בלי לספור חצאי-טונים באופן ידני. קיצורים דומים קיימים גם בפסנתר, אבל מכיוון שאני לא פסנתרן, אשאיר לכם למצוא אותם ברשת בכוחות עצמכם.
ועוד שאלה שוודאי תצוץ בראשכם במוקדם או במאוחר. מה יקרה אם תו השורש שלי נמצא, למשל, במיתר הראשון, הנמוך ביותר? במצב כזה, אני לא יכול "לרדת מיתר למטה"… ובכן, למזלנו, כל תו נמצא בכמה וכמה מקומות שונים על צוואר הגיטרה. למשל, התו C נמצא במיתר החמישי, שריג 3 – אבל גם במיתר השלישי, שריג 5, וגם במיתר הראשון, שריג 7! כל התווים האלה הם אותו התו – C: אפשר לנגן אותם כחלק מהאקורד והם יישמעו טוב באותה המידה. זו גם סיבה טובה עבורכם ללמוד את כל התווים על צוואר הגיטרה או קלידי הפסנתר.
האקורד המינורי
המבנה של האקורד המינורי דומה מאוד לזה של האקורד המז'ורי בהבדל אחד: התו השני הוא במרחק של טרצה קטנה (Minor 3rd) מהשורש, במקום טרצה גדולה. דהיינו:
התו הראשון, השורש, הוא התו המופיע בשם האקורד. למשל, באקורד Am (נכתב לעיתים כ Amin), השורש הוא התו A.
התו השני הוא התו במרחק של טרצה קטנה (שלושה חצאי טונים) מעל השורש. אם השורש הוא A, התו השני יהיה C.
התו השלישי הוא התו במרחק של קווינטה זכה (שבעה חצאי טונים) מעל השורש. אם השורש הוא A, התו השלישי יהיה E.
וכך מצאנו את כל שלושת התווים של האקורד המינורי. אגב, דרך אחרת – ואולי קלה יותר – למצוא את התווים של אקורד מינורי היא למצוא את התווים של האקורד המז'ורי בעל אותו השם (למשל, A במקום Am) – ואז, את התו השני להוריד בחצי-טון. בדוגמא של האקורד Am, התו השני של האקורד A (האקורד המז'ורי) הוא C#, ואם נוריד אותו בחצי טון, נקבל את התו C.
האקורד המוקטן (Diminished)
אקורדים מוקטנים יסומנו בדרך כלל כ dim (למשל, Gdim) או עם עיגול קטן מעל שם האקורד.
באקורד מוקטן, תו השורש יהיה התו בשם האקורד. לדוגמא, באקורד Gdim תו השורש הוא G.
התו השני יהיה במרחק של טרצה קטנה מעל השורש (משמע, שלושה חצאי טונים). באקורד Gdim, התו השני הוא Bb.
התו השלישי יהיה במרחק של קווינטה מוקטנת (שישה חצאי-טונים) מהשורש. באקורד Gdim, התו השלישי יהיה Db.
דרך אחרת למצוא את התווים של אקורד מוקטן היא להתחיל מהאקורד המז'ורי שלו (בדוגמא שלנו, G) ואז להוריד חצי-טון מהתו השני (= טרצה גדולה שהופכת לטרצה קטנה) וחצי-טון מהתו השלישי (קווינטה זכה שהופכת לקווינטה מוקטנת).
האקורד המוגדל (Augmented)
אקורדים מוגדלים מסומנים כ- aug (למשל, Faug) או עם + (F+).
התו הראשון הוא, כרגיל, השורש: F, בדוגמא שלנו.
התו השני הוא טרצה גדולה (ארבעה חצאי טונים) מעל השורש. עבור Faug, יהיה זה התו A.
התו השלישי הוא קווינטה מוגדלת (שמונה חצאי טונים) מעל השורש. עבור Faug, יהיה זה התו C#.
דרך אחרת למצוא את התווים האלה: להתחיל, כרגיל, מאקורד מזו'רי (F בדוגמא שלנו), ולהעלות את התו השלישי בחצי טון (מקווינטה זכה לקווינטה מוגדלת.)
סיכום
התחלנו את ההסבר בכך שכל אקורד בסיסי (טריאדה) עשוי משלושה תווים, ולמדנו איך למצוא את שלושת התווים האלה עבור כל אחד מארבעת הסוגים העקרוניים של אקורדים: מז'ורי, מינורי, מוקטן ומוגדל.
אבל אם תחשבו על זה, למדנו משהו אפילו חשוב ועקרוני מכך: למדנו שמה שחשוב באקורד הוא לא התווים הספציפיים מהם הוא עשוי – אלא המרווחים בין התווים המגדירים אותו. זו תובנה חשובה, מכיוון שמרווחים (Intervals) הם רעיון ששב ומופיע בכמעט כל מקום בתיאוריה המוזיקלית. בעזרת המרווחים, נתנו לאקורדים צורות קבועות – תבניות, כמו תבניות לחיתוך עוגיות – והמשמעות היא שבפעם הבאה שנתקל באקורד שלא ניגנו מעולם, נוכל לנגן אותו בקלות, על המקום! כל מה שצריך הוא למצוא על הפסנתר או הגיטרה את תו השורש – ולהציב את האצבעות שלנו במרווחים הידועים והמוכרים.
איך ללמוד היטב
הקדמה
'עושים היסטוריה', הפודקאסט שהקמתי לפני כשלוש עשרה שנה, עוסק במגוון רחב מאוד של נושאים: ממחשבים קוונטיים, דרך הפילוסופיה של דקארט ועד מלחמת יום הכיפורים. קשה לי לחשוב על תחום מדעי\תרבותי\טכנולוגי שלא נגעתי בו לפחות פעם אחת במסגרת הפודקאסט. בכל פרק, אני נדרש לצלול לעומקו של הנושא הנבחר ולכתוב עליו – בתוך שבועיים, בדרך כלל – חיבור בהיקף של כ-4000-5000 מילים, שיעביר באופן בהיר ומעניין את עקרונות היסוד של התחום המדובר.
כפועל יוצא של המקצוע התובעני שבחרתי לעצמי, התמקצעתי במרוצת השנים בלימוד יעיל ומהיר יחסית של חומר חדש. ולפני שאתם קופצים למסקנות: אני לא חכם. זאת אומרת, אני חושב שיש לי מידה סבירה של אינטליגנציה, אבל אני לא חכם יותר מהאדם הממוצע. אף פעם לא הייתי תלמיד מצטיין בבית הספר או באוניברסיטה. אני חושב שאני חב את יכולת הלימוד שלי לשנים רבות של ניסיון מצטבר במסגרות רבות: מקורס חובלים של חיל הים, דרך לימודי הנדסת חשמל בטכניון, שלושת ספרי העיון שכתבתי – וכאמור, הניסיון העשיר שצברתי בעבודה על הפודקאסט.
מטרתי במאמר הזה היא לזקק את העקרונות החשובים וטכניקות הלימוד שרכשתי בזכות הניסיון הזה, כדי שאתם תוכלו ליהנות מפירותיו כבר היום. ראוי לציין שלא המצאתי אף אחת מהטכניקות שאתאר כאן: את רובן "ליקטתי" במרוצת הזמן ממורים או מספרים שקראתי. מתוך אותם רעיונות ועקרונות שספגתי, בחרתי להביא כאן את אלה שמצאתי הכי שימושיים.
1. לכל אדם יש את שיטת הלימוד המתאימה לו ביותר
(עדכון, 3.9.21: להרחבה בנושא המחקר המדעי בתחום שיטות הלימוד המועדפות – ראו נספח א' בתחתית המאמר)
כשאני מספר לאנשים שהייתי תלמיד די בינוני בבית הספר ובטכניון, אני בדרך כלל מקבל תגובות מופתעות. חלק מהאנשים בטוחים שאני סתם מנסה להצטנע – אבל הציונים שלי היו באמת בינוניים למדי. במתמטיקה, למדתי בארבע יחידות (והייתי קרוב מאוד לרדת לשלוש יחידות) – והמורה שלי לפיסיקה בתיכון המליץ לי לנטוש את המקצוע ולעבור למשהו קל יותר… ניסיתי. באמת שניסיתי. הייתי תלמיד 'חרשן', הקפדתי על שיעורי בית ולא נעדרתי מבית הספר – ובכל זאת, תמיד הייתי בינוני. כמו רוב בני הנוער במצבי, השתכנעתי ש"אין לי את זה." שאני לא טוב בלימודים, ואין מה לעשות.
את הסיבה האמיתית לבינונית הפדגוגית שלי גיליתי במקרה לגמרי, בשנה הרביעית ללימודי בטכניון. מישהו סיפר לי שחלק מההרצאות של הפקולטה הוקלטו בוידיאו, וניתן לצפות בהן בחדר צפיה מיוחד. החלטתי לבדוק את העניין. ניגשתי לחדר הצפיה, בחרתי קלטת של הרצאה כלשהי והתיישבתי מול המסך.
כמעט מייד חשתי בשינוי. הבעיה הגדולה ביותר שלי בלימודים, מאז שאני זוכר את עצמי, היא שאף פעם לא הצלחתי לעקוב אחר הסבריו של המורה. המורים דיברו מהר מדי בשבילי, ואני לא הייתי מסוגל לכתוב את מה שהם רושמים על הלוח – וגם להבין, במקביל, על מה הם מדברים. אבל לפתע פתאום, מול מסך הטלוויזיה בחדר הוידאו, כבר לא הייתי מוכרח לבחור: יכולתי להאזין למרצה, לעצור את הקלטת, 'לעכל' את הדברים ולהבין אותם – ורק אז להעתיק אותם אל המחברת שלי, כשאני כבר מבין טוב יותר על מה מדובר.
הצפייה בהקלטות הוידאו שינתה את חוויית הלימוד שלי באופן דרמטי. נכון: לקח לי פי שתיים יותר זמן לעבור על הרצאה בוידאו מאשר אותה הרצאה בזמן אמת, בכיתה – אבל בניגוד להרצאות בכיתה, כשסיימתי לצפות בקלטת הבנתי את החומר. הרגשתי שפיסות הפאזל שהמרצה מנסה ללמד אותנו סוף סוף מתחברות אצלי בראש לכדי הבנה עמוקה ואמיתית של החומר הנלמד, רמת הבנה שלא זכיתי לה בכל שלוש שנות הלימודים הקודמות שלי. עד מהרה הפסקתי ללכת לגמרי להרצאות הפרונטליות, ולמדתי אך ורק מול הוידיאו. ולמרות שלא הגעתי לכמעט אף הרצאה – ממוצע הציונים שלי באותה השנה זינק בעשר עד עשרים נקודות יותר מזה של השנים הקודמות. לפתע פתאום, כבר לא הייתי בינוני!
הניסיון הזה לימד אותי לקח חשוב: לא כולם מסוגלים ללמוד באותה הדרך.
במבט לאחור, העיקרון הזה נראה לי כמעט מובן מאליו. הרי ברור שלכל אחד מאיתנו יש חוזקות וחולשות אינדיוידואליות. יש אנשים שיש להם כישרון ציור מופלא, אבל הם נהגים גרועים. יש אנשים שהם שחקני כדורגל מדהימים אבל קשה להם להתבטא מול המיקרופון, ויש אנשים שמסוגלים לפתור משוואות מורכבות בקלות – אבל לא היו מסוגלים לדפוק מסמר ישר בקיר גם אם חייהם היו תלויים בכך. אנחנו מקבלים את קיומן של אותן חוזקות וחולשות אנושיות בכמעט כל תחום – אבל משום מה, ההבנה הזו לא מחלחלת אל האופן שבו אנחנו מלמדים את הילדים שלנו. בכל ימי כתלמיד, הן בבית הספר והן באוניברסיטה, לא נתקלתי ולו פעם אחת במורה שהתייחס בצורה ישירה לחוזקות ולחולשות האינדיבידואליות שלנו כתלמידים. אף אחד מעולם לא אמר לי – 'שמע, עושה רושם שקשה לך להבין על מה המורה מדבר בכיתה: אולי תנסה ללמוד את החומר מספר?' זה פשוט לא קרה.
במקרה שלי, אם כן, גיליתי ששינוי פעוט באופן הלימוד – למידה איטית מתוך סרטון וידאו, במקום לימוד פרונטלי בכיתה – שיפר את יכולת הקליטה שלי באופן משמעותי. התגלית הזו שירתה אותי נאמנה גם בהמשך חיי, כשהגיח יוטיוב לחיינו.
ומה אתכם? האם הקדשתם מחשבה לשאלה איזו שיטת לימוד מתאימה לכם? אחרי הכל, בימינו – יש לא מעט אפשרויות לבחור מהן, מעבר לכיתה המסורתית ובה מורה אחד וכמה עשרות תלמידים. סרטונים, פודקאסטים, ספרים, בלוגים, מורה פרטי, קבוצות למידה באינטרנט… כל כך הרבה דרכים לצרוך ידע! סביר להניח שלפחות אחת משיטות הלימוד האלה תתאים לכם יותר מהאחרות, ואתם עשויים לגלות שחוויית הלימוד שלכם משתנה מהקצה אל הקצה: במקום שהלימוד יהיה עול משעמם וטרחני, תמצאו את עצמכם נהנים מחדוות הגילוי ומתחושת ההעצמה שמתלווה לידע חדש.
אם כן, אל תניחו שרק מכיוון שכל חייכם הורגלתם ללמוד בדרך מסוימת – זו גם דרך הלימוד הנכונה ביותר עבורכם. נסו שיטות לימוד נוספות, ואולי תגלו אחת שמסיבה כלשהי מתאימה טוב יותר למבנה המוח ולחוזקות האישיות שלכם. מכל העצות והרעיונות שאביא כאן, זו אולי העיצה שעשויה להביא לכם את התועלת הגדולה ביותר בטווח הארוך.
2. לא כל המורים נולדו שווים
המורה שלי למתמטיקה בתיכון לא הייתה מורה טובה. לא ידעתי את זה אז, כמובן: הייתי נער בן 16 שמעודו לא נתקל במושגים כגון 'אינטגרל' או 'דיפרנציאל' – ומכיוון שהיה ברור כשמש שהמורה מבינה את המושגים האלה על בוריים, הנחתי שהסיבה שאני לא מבין אותם היא מכיוון שאני "לא טוב במתמטיקה."
מספר שנים לאחר מכן, החלטתי להשלים בגרות במתמטיקה לחמש יחידות כדי להתקבל לטכניון. הכנתי את עצמי נפשית למסע הייסורים שחוויתי במקצוע הזה בימי בתיכון, ולאינספור שעות של פתירת תרגילים משמימים כדי להכניס לעצמי את הידע הדרוש "דרך הרגליים."
אבל כבר מהשיעור הראשון הבנתי שנקלעתי לעולם אחר. המורה שלי בקורס, מוחמד שמו, לימד אותנו את אותו החומר שלמדנו בתיכון – אבל בצורה אחרת לגמרי! אין טעם להכנס לפרטים לגבי האופן הספציפי שבו לימד אותנו את החומר (הרחבתי על כך בסדרת המאמרים על 'איך ללמד חומר מורכב') – אבל השורה התחתונה הייתה שעם מוחמד, הבנתי הרבה יותר טוב את אותו החומר שלא הצלחתי להבין כשהייתי תלמיד בתיכון.
(כהערת אגב, ראוי לציין שבאותו הזמן כבר הייתי מבוגר יותר בשש שנים מכפי שהייתי בתיכון, וייתכן שהיייתה לכך השפעה כלשהי גם על יכולת הלימוד שלי – אבל לתחושתי, הגיל שיחק תפקיד מינורי מאוד, אם בכלל. שיטת הלימוד השונה של מוחמד פשוט התאימה לי הרבה יותר משיטת הלימוד של המורה בתיכון.)
כמו בסעיף הקודם, במבט לאחור זה נראה כמו דבר מובן מאליו. יש אינסטלטור מצוין, ויש אינסטלטור בינוני. יש רופא נפלא ורופא קצת פחות נפלא. יש כדורגלנים סבירים – ויש את מסי, מארדונה ופלה. מדוע שתחום ההוראה יהיה שונה? והוא לא, כמובן. יש מורים טובים – ויש מורים יותר טובים.
עצתי לכם, אם כן, היא לא לקבל את המורה שזימן לכם הגורל כגזירה משמיים. אם אתם מרגישים שהמורה שלכם לא מתאים לכם – נסו לעבור לכיתה אחרת. אם אין מורה אחר, נסו להעזר בתלמיד אחר שיסביר לכם את החומר המדובר. אם אפשר, חפשו קורס מקוון ביו-טיוב כדי ללמוד את החומר במקביל לשיעורים הפרונטליים. אל תתפשרו על המורה שלכם.
3. להבין – במקום לשנן
כשזה מגיע לשינון ולמידה בעל פה, אני ממש לא רע. אחרי שנים של הרצאות בפני קהל מגוון, הגעתי למצב שאני מסוגל ללמוד בעל פה הרצאה של שעה בתוך כמה שעות ספורות של תרגול. ובכל זאת, אני חושב ששינון הוא צורת הלימוד הגרועה ביותר שאני מכיר. בידקו את עצמכם: כמה מתוך עשרות התמרורים שלמדתם בעל פה כשהתכוננתם למבחן התיאוריה של רשיון הנהיגה, אתם עדיין זוכרים? כמה מתוך הנוסחאות המתמטיות ששיננתם בתיכון אתם עדיין יכולים לשלוף על המקום? אם אתם כמוני, כנראה שהתשובה תהיה זהה בשני המקרים: לא הרבה. ידע שנרכש באמצעות שינון הוא ידע נדיף מאוד, שנעלם מממוחנו באותה המהירות שבה נכנס לתוכו.
הבנה, לעומת זאת, היא צורת הלימוד היעילה והמתגמלת ביותר. דברים שהבנתי לעומק נשארו איתי במשך שנים רבות, גם אם השתמשתי בידע הזה לעיתים נדירות בלבד.
השאלה המתבקשת, כמובן, היא – מהי "הבנה"? מתי אנחנו יכולים לדעת שאנחנו באמת מבינים משהו, ולא רק זוכרים אותו בעל פה? התשובה היא: כשאנחנו מסוגלים להשיב על השאלה "למה?".
ניקח, כדוגמה, את עניין התמרורים. מה ההבדל בין תמרור משולש ובו ציור של אופניים, לתמרור עגול ובו אותו הציור בדיוק? תשאלו מישהו שלומד ברגע זה למבחן התיאוריה, והוא בטח יידע את התשובה: התמרור המשולש אומר 'הזהר, רוכבי אופניים בסביבה', והתמרור העגול מתריע כי הכניסה לרוכבי אופניים אסורה. אבל אם תשאלו אותו 'למה?'… זה כבר עניין אחר. כדי לענות על השאלה 'למה', יש להבין שבישראל, תמרור משולש מציין 'אזהרה', ותמרור עגול מציין איסור, או הגבלה. זו מידת הבנה שהיא רמה אחת מעל שינון סתמי של כל התמרורים השונים – וקל לראות עד כמה היא שימושית. אם אבין את משמעותם העקרונית של המשולש והעיגול בתמרורים – כנראה שאוכל לפענח את משמעותם של עוד כמה עשרות תמרורים, רק מתוך הציורים שבתוך המשולש או העיגול – ויש סיכוי טוב שאוכל לעשות זאת גם חמש או עשר שנים אחרי שלמדתי לתאוריה.
אותו העיקרון תקף בכמעט כל תחום ידע. נוסחאות ומשוואות פיזיקליות, למשל, נראות מורכבות ומסובכות – עד שמבינים את משמעותן, דהיינו – את פשר הרעיונות העמוקים שאותן הן מייצגות. ברגע שמבינים את הרעיונות האלה, הנוסחה מפסיקה להיות אוסף של אותיות אקראיות – והופכת להיות מובנת בדיוק באותו האופן שבו המילים שאתם קוראים ברגע זה אינן אוסף של אותיות אקראיות, כי אם ייצוגים טקסטואליים של מושגים ורעיונות.
דוגמה נוספת לאותו העיקרון היא לימוד של מונחים מקצועיים מסובכים. מונחים רפואיים הם דוגמה קלאסית: אפידרמיס, היפוגליקמיה, פרוגנוזה… לסטודנט שרק מתחיל את צעדיו בעולם הזה, אני מניח שכל המונחים האלה הם כאב ראש ענק. אפשר ללמוד אותם בעל פה, כמובן – אבל אם שכנעתי אתכם שהבנה עדיפה על פני שינון, כדאי לחפש דרך אחרת. ויש כזו: למרות שמונחים מקצועיים עשויים להראות כשרירותיים לחלוטין (ולפעמים, הם באמת שרירותיים), במקרים רבים יש מאחורי השמות הגיון סמוי. בתחום הרפואה, למשל, מרבית המונחים מכילים בתוכם תחיליות וסופיות סטנדרטיות שמגיעות מלטינית, יוונית או אנגלית. "אפי" זה מעל. "היפו" זה מתחת. "פרו" לזה לפני. אם נשקיע מאמץ מכוון ללמוד את אותה כמות מוגבלת של תחיליות וסופיות – נוכל לפענח בעצמנו את משמעותם של המונחים, גם אם לא נזכור אותם בעל פה באופן מושלם.
בשורה התחתונה, אם כן: הבינו את הרעיונות העמוקים, ולא תצטרכו ללמוד דבר בעל פה.
4. ללמד כדי ללמוד
בסעיף הקודם למדנו שהבנה עדיפה בהרבה על פני שינון. בסעיף זה נגלה איך להגיע אל אותה 'הבנה' באופן המהיר והיעיל ביותר.
תרשו לי להעזר מניסיוני העגום כמפתח תוכנה. אחת החוויות המתסכלות עבור כמעט כל מפתח תוכנה, היא Debugging – איתור ותיקון שגיאות בקוד. לא אחת יצא לי לשבור את הראש על תקלה משונה בקוד תוכנה, להביט שעות באותה פיסת טקסט על המסך ולא להתקדם אפילו במילימטר.
טכניקה מקובלת בעולם התוכנה להתמודד עם אתגר הדיבאגינג היא זו המכונה 'ברווז גומי' (Rubber Duckking). הרעיון הוא כזה: כשאתה נתקל בבעיה כלשהי בתוכנה ולא מצליח להבין את מקורה, עליך לדמיין שיש לצידך מתכנת אחר – לצורך העניין, "ברווז גומי" היפוטתי שיושב מול על השולחן – ועליך להסביר לו איך עובדת התוכנה שכתבת, לפרטי פרטים. אתה והברווז עוברים על הקוד שורה אחר שורה, ומתעכבים על הרעיונות הבסיסיים והנחות היסוד שעל פיהן עבדת, ואת הגורמים לכל החלטה והחלטה שקיבלת לאורך הדרך.
אני יודע, זה נשמע קצת אידיוטי – ויש סיכוי שאם תדבר אל ברווז גומי אמיתי, עמיתיך למשרד יתחילו להתעניין אם הכל בסדר בבית – אבל בחיי, זה עובד. ברובם המכריע של המקרים, תוך כדי תהליך ההסבר הזה – גיליתי את השגיאה שחמקה ממני עד אותו הרגע.
מדוע שיטת ברווז הגומי עובדת? ברור שלברווז ההיפוטתי והפאסיבי שלנו אין קשר להצלחה. השיטה עובדת מכיוון שכחלק מתהליך ההסבר של הקוד, אתה מוכרח לנסח במילים ברורות ומפורשות את כל אותן רעיונות והנחות יסוד שהובילו אותך לאורך הדרך. עצם הניסוח המפורש שלהן מציף על פני השטח כשלים ובעיות שעד כה אולי פיספסת או התעלמת מקיומם, ורק עכשיו הם חזרו כדי למרר את חייך.
אותה הטכניקה, מסתבר, עובדת נהדר כשאנחנו רוצים ללמוד משהו חדש. נניח שסיימתי לקרוא את החומר, לצפות בסרטון ההדרכה או שאני מתכונן למבחן. אני אקח דף ועט ואתחיל לבנות מעין 'מערך שיעור' וירטואלי, כאילו שאני מלמד ברווז גומי דמיוני.
אתחיל מהגדרת המטרה: מה בדיוק אני רוצה ללמד? מהו העיקרון או הרעיון החדש, ומדוע בכלל הוא חשוב או רלוונטי? לאחר מכן, אני פורש בצורה מפורשת את הנחות היסוד או הרעיונות המקדימים החשובים לעניין, ומשם אני מתקדם צעד אחר צעד ומסביר לתלמיד ההיפותטי שלי כל שלב, רעיון חדש או היסק לוגי. וכצפוי, תוך כדי תהליך ההסבר אני אתקל בכל אותם פערי ידע וחוסרים בהבנה שדילגתי עליהם ממקודם – אולי מכיוון שהייתי עסוק בהעתקה מהלוח או מכל סיבה אחרת. כשהתלמיד הוירטואלי שלי ישאל אותי 'אבל למה?…' אני אהיה חייב להעמיק את ידיעותי כדי להיות מסוגל לענות לו, לעיתים עד חזרה לעקרונות היסוד והרעיונות הבסיסיים ביותר של התחום אותו אני מעוניין ללמוד – ובכך טמונה עוצמה של הטכניקה הזו.
אגב, אני מוצא המון דימיון בין הטכניקה הזו ובין שיטת הלימוד שהייתה מקובלת בימים שלפני הופעתו של בית הספר המודרני, אי שם בימי המהפכה התעשייתית: התמחות באמצעות שולייה (Apprenticeship). מי שרצה ללמוד נגרות היה הולך להיות שולייה של נגר, ומי שביקש להיות צייר היה הופך לשולייה של צייר מנוסה. בתחילה השולייה היה רק צופה במאסטר עושה את עבודתו ולומד מההסברים – אבל בשלב מסוים הוא נדרש גם לבצע את הדברים בפועל: לבנות שולחן או לצייר פורטרט תחת עינו הבוחנת של איש המקצוע. תוך כדי הביצוע בפועל, התלמיד היה מגלה את הפערים בידע שצבר – והמאסטר היה משלים את החוסר הזה. בשיטה שתיארתי, אנחנו משמשים פעם אחת כתלמיד – בזמן שאנחנו לומדים וסופגים את החומר באופן פאסיבי – ופעם אחרת כמאסטר, בזמן שאנחנו מלמדים את אותו החומר ומתרגלים אותו.
סיכום
במאמר זה פרשתי בפניכם שלוש עקרונות, או שלוש טכניקות, שסייעו לי ללמוד טוב יותר.
- זיהוי שיטת הלימוד המתאימה לי ביותר,
- בחירה אקטיבית של מורה טוב,
- העדפה של הבנה על פני שינון עיוור, ו-
- ללמד כדי ללמוד: יצירת מעין 'מערך שיעור' וירטואלי כדי לזהות פערי ידע.
את הרעיון הראשון, זיהוי שיטת הלימוד המתאימה לנו ביותר, לא תמיד קל ליישם אותו בגיל צעיר. לפעמים, אנחנו צריכים קצת ניסיון חיים כדי להכיר את עצמנו טוב יותר ולגלות מה עובד לנו ומה לא. אף על פי, כדאי לכל הפחות להיות מודעים לחשיבותה של הנקודה הזו כבר בשלב מוקדם.
את שלושת הטכניקות האחרות שהצעתי אתם יכולים ליישם כבר עכשיו, בכל גיל! המשותף להן הוא השקעת זמן ומאמץ בשלב הראשון של הלימוד, כדי לחסוך הרבה יותר זמן בטווח הארוך. אין ספק שהתעמקות והבנה, למשל, דורשות מאמץ מחשבתי אחר ואולי מאתגר יותר מ'סתם' שינון עיוור – אבל בטווח הארוך, שינון היא טכניקת לימוד גרועה וחסרת תועלת: כמעט תמיד אנחנו נשכח את מה שלמדנו, ובכך "נבזבז" את הזמן והמאמץ שהשקענו בלימודים, לחינם…
אני מקווה שהרעיונות שפרשתי בפניכם יעזרו לכם להנות מהלימודים! 🙂
רן
נספח א' – המחקר המדעי בתחום שיטות הלימוד המועדפות
מספר קוראים הפנו את תשומת ליבי למחקרים שהראו שקרוב לוודאי שהרעיון של שיטת לימוד מועדפת הוא מיתוס, ובניסויי סמיות כפולה (Double Blind) הוכח כי אין הבדל בין ביצועי סטודנטים שלמדו בשיטות שונות. ערוץ היו-טיוב הנהדר Veritasium סקר את המיתוס המדובר ואת המחקרים שנעשו סביבו בסרטון כאן.
תחת ההנחה שהמחקרים בתחום אמינים – מהו ההסבר לניסיון האישי שלי? ברשותם, אציע שני הסברים אפשריים.
- על פי המתואר בסרטון, רוב המחקרים נעשו על סטודנטים, שנשאלו לגבי שיטת הלימוד המועדפת עליהם. הדגשתי את המילה 'מועדפת' מכיוון שאני מתייחס למשהו מעט שונה: שיטת הלימוד המתאימה ביותר. יש הבדל בין שני המונחים האלה! ייתכן וסטודנטים, בשל גילם הצעיר, אינם מנוסים מספיק ואינם מכירים את עצמם מספיק טוב בשביל לדעת מהי שיטת הלימוד המתאימה להם. הם חושבים שהם יודעים -ולכן הם מעדיפים את שיטה X על פני שיטה Y – אבל הם טועים מפאת חוסר ניסיונם. כשאני הייתי סטודנט, למשל, חשבתי ששיטת הלימוד המתאימה לי היא קריאה מספר – אבל עם השנים למדתי שדווקא לימוד מסרטוני וידיאו היא השיטה המתאימה לי ביותר.
- ייתכן שבמקרה הפרטי שלי, מה ששיחק תפקיד משמעותי במיוחד אינו בהכרח האלמנט של לימוד ויזואלי על פני לימוד לא-ויזואלי, אלא עניין קצב הלימוד. כפי שציינתי במאמר, כשלמדתי מול המסך, יכלתי לעצור את הוידיאו, לעכל את הנאמר, ואז להמשיך בסרטון – וזה, לתחושתי, גדול מאוד ממה שסייע לי בלימודים! הבעיה שלי עם הלימוד הפרונטלי הייתה שהקליטה שלי לא הייתה מספיק מהירה כדי לעמוד בקצב של שאר הכיתה – ולימוד מול וידיאו פתר את הבעיה הזו לחלוטין. במילים אחרות – ייתכן שהאלמנט הויזואלי שיחק תפקיד פחות מהותי מאשר היכולת להאט את קצב הלימוד. זה משהו שלמיטב הבנתי לא נבדק במסגרת המחקרים המדוברים.
גם אם המחקרים צודקים, עצתי – מתוך ניסיוני האישי – היא בכל זאת להמשיך ולבחון את עצמכם כדי לגלות את שיטת הלימוד המועדפת עליכם. מדוע? ראשית, מכיוון שתחום המחקר הזה עודנו בחיתוליו: אנחנו לא מכירים מספיק טוב את המוח האנושי כדי להגיע למסקנות סופיות ומוחלטות, ויש לי תחושה שיש עוד דברים שאנחנו לא מבינים על איך המוח שלנו לומד דברים. ושנית, כל מחקר הוא עניין של סטטיסטיקה: גם אם, למשל, רוב הנבדקים לא הראו שונות כזו או אחרת ביכולת הלימוד שלהם בצורות שונות – זה לא אומר שאתם (כמוני) נופלים בחתך הסטטיסטי הזה.






